Список секций и кружков: Кружки для детей ✔️ Какие бывают, список
как получить сертификат на бесплатные кружки и секции
Родители привыкли, что в садике и школе учат только самому основному. Если хочется отдать ребёнка куда-то ещё — на английский или в секцию самбо — придётся заплатить из своего кармана. На самом деле, даже дошкольники могут бесплатно ходить на дополнительные занятия. За всё платит государство, а родителям остаётся только оформить сертификат и выбрать кружок.
Детские кружки можно посещать бесплатно. Фото: azr73.ru
Что такое сертификат ПФДО
ПФДО расшифровывается как персонифицированное финансирование дополнительного образования. Это именной электронный сертификат, с помощью которого можно оплачивать дополнительное образование детей — будь то спортивные секции, ментальная арифметика, кружок ИЗО или бисероплетения. Он выдаётся с 2019 года в рамках федерального проекта «Успех каждого ребёнка».
Систему сертификатов ввели, чтобы финансирование дополнительного образования в России стало прозрачным. Уже не получится фиктивно записать детей в кружки, зато востребованные направления будут развиваться. Кроме того, с помощью сертификатов государство может отследить, на какие занятия ходят дети, и оплачивать работу педагогов в зависимости от нагрузки.
Уже не получится фиктивно записать детей в кружки, зато востребованные направления будут развиваться. Кроме того, с помощью сертификатов государство может отследить, на какие занятия ходят дети, и оплачивать работу педагогов в зависимости от нагрузки.
Сертификат полагается детям от 5 до 17 лет включительно — дошкольникам старшего возраста и школьникам.
Пока сертификаты выдают не во всех регионах. Например, их можно оформить в Московской, Ленинградской, Владимирской и Кировской областях, Приморском крае, Удмуртской Республике, ХМАО — полный список есть на порталах ПФДО и АИС «Региональный навигатор дополнительного образования Inlearno». Но до конца 2024 года программа заработает по всей стране.
Какие кружки можно посещать
Кружки и секции подают заявку на участие в оплате сертификатами. Чиновники проверяют лицензию на дополнительное образование, оценивают качество и востребованность услуги. Если занятия соответствуют требованиям госпрограммы, этот кружок включают в специальный реестр.
Но в программе участвуют далеко не все коммерческие детские центры. Например, популярной танцевальной школе нет смысла принимать сертификаты, потому что спрос на занятия и так высокий.
Бесплатно можно посещать занятия практически по всем направлениям:
- физкультурно-спортивное — шашки и шахматы, футбол, плавание, лёгкая атлетика, баскетбол, волейбол, конькобежный спорт, хоккей, карате, фехтование, самбо, дзюдо, бокс, спортивная акробатика;
- социально-гуманитарное — школа раннего развития, русский и иностранные языки, литература, журналистика, профессиональное самоопределение, воспитание патриотизма, финансовая грамотность, экономика, кулинария;
- естественно-научное — юный натуралист, занимательная химия, физика, география, астрономия и биология, первая медицинская помощь;
- художественное — театральная студия, музыка, хоровое пение, танцы, живопись, литературное творчество, фотография, школа циркового мастерства, театр моды, моделирование одежды;
- туристско-краеведческое — юный краевед, пешеходный и спортивный туризм, традиции народа, скауты, спелеология, школа экскурсовода, начальная военная школа, музейный клуб;
- техническое — IT-технологии, робототехника, конструирование и моделирование, юный инженер, компьютерная грамотность, школа программирования.

Какие именно кружки будут доступны вам, полностью зависит от муниципалитета. В кружках с востребованными направлениями мест может не хватать — например, английский или программирование. А вот заниматься шахматами и хоровым пением обычно мало желающих.
Как получить сертификат
Сертификаты выдают муниципальные власти, они же определяют правила их использования и номинал. Разница может быть существенной. В одном регионе на весь год на ребёнка выделяют 10 000 ₽, а в другом — всего 3000 ₽.
Родители оформляют сертификат на «Госуслугах» или портале ПФДО. Там же он и будет храниться — на руки документ не выдают. Заявку могут подать официальные представители — родители, опекуны — или сам ребёнок старше 14 лет.
Как получить сертификат на «Госуслугах»:
- Зайдите на сайт под своей учётной записью.
- Если в профиле не указаны дети, введите их ФИО, дату рождения, данные СНИЛС и свидетельств о рождении.
- Через поиск на сайте найдите программу ПФДО и выберите кружок.
 Рядом с ним должна быть отметка, что запись открыта и возможна оплата сертификатом. Запись в кружки доступна не всегда. Например, в них может не быть свободных мест или ребенок не подходит по возрасту — придется выбирать из оставшихся.
Рядом с ним должна быть отметка, что запись открыта и возможна оплата сертификатом. Запись в кружки доступна не всегда. Например, в них может не быть свободных мест или ребенок не подходит по возрасту — придется выбирать из оставшихся. - Изучите правила приёма и запишите ребёнка в кружок. Например, для занятий плаванием или в секцию спортивной гимнастики потребуется справка о здоровье, а занятия компьютерным дизайном могут быть предназначены для детей старше 12 лет.
- Уведомление о том, что запись подтверждена, придёт в течение недели.
Сертификат выпишут автоматически — он будет действовать до совершеннолетия ребёнка. Но его ещё нужно активировать: прийти в школу, гимназию или детский центр из предложенного списка. Родителю надо взять с собой паспорт, свидетельство о рождении, СНИЛС и прописку ребёнка. Школьники старше 14 лет могут активировать сертификат без родителей.
Организатор кружка может попросить вас подойти лично, чтобы подтвердить запись. Но обычно всё происходит удалённо — родителям остаётся только подписать договор на дополнительные занятия.
Иногда для записи надо пройти вступительные испытания. Например, спортивная секция предполагает определённый уровень подготовки — тренеру нужно оценить, что умеет ребёнок, и только после этого он примет решение о приёме. На подтверждение должно уйти не более 45 дней.
В посещении кружка могут отказать, но на это должна быть объективная причина. Например, ребёнок не подходит по здоровью — у него плоскостопие, а родители хотят записать его в секцию спортивного бега. Если вы считаете, что отказали необоснованно, можно оставить жалобу на сайте правительства своего региона.
Если вы переезжаете в пределах того же региона, просто продолжайте пользоваться сертификатом. Если же новое место жительства находится в другом крае или области, надо «заморозить» сертификат и после переезда получить новый. Это связано с тем, что финансирование идёт за счёт муниципалитета.
Иногда школы и детсады требуют зарегистрировать детей на сайте ПФДО, чтобы оплата внутренних кружков и секций шла за счёт сертификатов. Бывает, что и занятия ребёнок не посещает — его фиктивно зачисляют ради финансирования и наполняемости кружков. Помните, что это незаконно — выбирать дополнительные занятия имеют право только родители. На сайте ПФДО можно проверить, куда записан ребёнок. К тому же родителям на электронную почту, указанную при подаче заявления, приходят уведомления о зачислении в кружок или секцию.
Бывает, что и занятия ребёнок не посещает — его фиктивно зачисляют ради финансирования и наполняемости кружков. Помните, что это незаконно — выбирать дополнительные занятия имеют право только родители. На сайте ПФДО можно проверить, куда записан ребёнок. К тому же родителям на электронную почту, указанную при подаче заявления, приходят уведомления о зачислении в кружок или секцию.
Как оплачивать занятия
Деньги на оплату кружков и секций идут из муниципального бюджета. Их зачисляют на сертификаты один или два раза в год — например, в январе и перед 1 сентября. Средства нужно потратить в течение текущего календарного года, иначе 31 декабря они «сгорят», то есть вернутся в бюджет. На следующий год они не переносятся и обналичить их нельзя.
При этом муниципалитет выделяет на сертификаты ПФДО определённую сумму, которой может не хватить всем желающим. Поэтому записываться на кружки лучше заранее — например, в мае — чтобы к началу учебного года на сертификат зачислили деньги.
За каждое занятие будет списываться плата. Проверять баланс сертификата, поступления и списания можно на «Госуслугах» или портале ПФДО. Здесь же видно, в какие секции и кружки зачислен ребёнок.
Если вы записали ребёнка сразу в несколько секций, денег на сертификате может не хватить. Тогда придётся доплачивать из собственных средств.
Также по сертификатам ПФДО может быть ограничено количество программ — уточните, какие правила действуют в вашем регионе. Обратите внимание, что кружок и программа — это разные понятия. Один кружок может реализовывать несколько образовательных программ. Например, существует лимит — не более 9 программ на ребёнка. В кружке моделирования одежды есть несколько направлений: кройка и шитьё, дефиле, конструирование. Значит, за этот кружок с сертификата спишут сразу 3 программы. Свой лимит предусмотрен для платных и бесплатных кружков.
Если ребёнку не понравились занятия, от них можно отказаться в любой момент — в самом кружке, через личный кабинет на «Госуслугах» или «ПФДО». Но не забудьте расторгнуть договор, иначе с сертификата так и будут списывать деньги.
Но не забудьте расторгнуть договор, иначе с сертификата так и будут списывать деньги.
Бесплатные секции и кружки для детей в Новосибирске: как записать ребенка август-сентябрь — 9 августа 2022
А ваш ребенок ходит на какие-нибудь секции? Поделитесь в комментариях
Фото: Александр Ощепков
Поделиться
Многие родители уже задумываются, чем занять ребенка во время учебного года. В Новосибирской области через специальный сайт можно выбрать бесплатные кружки и секции для детей. Что такое «сертификат дополнительного образования» и зачем он нужен, мы подробно рассказали в 6 простых карточках. А сегодня поделимся с вами актуальным списком из 50 крутых бесплатных кружков для детей в Новосибирске, в которых пока еще есть свободные места. Изучайте и выбирайте (данные приведены на момент публикации).
Больше всего предложений в спортивной сфере. Детей записывают на борьбу, волейбол, баскетбол, зимние виды спорта. Но есть и очень необычные направления.
Но есть и очень необычные направления.
Для детей доступны бесплатные занятия конным спортом
Фото: Александр Ощепков
Поделиться
1. Фехтование
Спортивная школа олимпийского резерва по фехтованию.
- адрес: ул. Гаранина, д. 2;
- телефон: (383) 349–98–86.
Для детей от 8 до 17 лет.
2. Паркур
Центр внешкольной работы «Галактика».
- адрес: пр. Дзержинского, д. 83;
- телефон: (383) 279–75–73.
Идет запись в утреннюю группу. Для детей от 11 до 17 лет.
3. Конный спорт
Спортивная школа по конному спорту.
- адрес: Тулинский, ул. Тимирязева 3/6; 1-я Чулымская 112/1 к.1;
- телефон: 8–923–737–38–77
Занятия проводятся 3 раза в неделю по утрам. Для детей от 10 до 18 лет.
4. Настольный теннис
Центр детского творчества Советского района.
- адрес: ул. Приморская, д. 3;
- телефон: (383) 330–25–71.
Для детей от 6 до 13 лет.
5. Бильярдный спорт
Спортивная школа технического, экстремального, интеллектуального спорта.
- адрес: ул. Вокзальная магистраль, д. 16;
- телефон: (383) 209–23–05.
Занятия проводятся 4–6 раз в неделю. Для детей от 7 до 18 лет.
Секция керлинга ждет юных спортсменов
Фото: Александр Ощепков
Поделиться
6. Прыжки на батуте
Спортивная школа олимпийского резерва по гимнастическим видам спорта.
- адрес: ул. Лермонтова, д. 47;
- телефон: (383) 328–33–84.
Занятия проводятся 3–6 раз в неделю. Для детей от 7 до 18 лет.
7. Киберспорт
Спортивная школа олимпийского резерва по стрелковым видам спорта.
- адрес: ул. Ватутина, д. 41/1;
- телефон: (383) 200–35–82.

Занятия проводятся 3 раза в неделю. Для детей от 12 до 19 лет.
8. Рафтинг
Спортивная школа технического, экстремального, интеллектуального спорта.
- адрес: ул. Тенистая, д. 20;
- телефон: (383) 209–23–05.
Занятия проводятся 3–6 раз в неделю. Для детей от 10 до 18 лет.
9. Чирлидинг
Центр детского творчества «Содружество».
- адрес: ул. Новоуральская, д. 19/12;
- телефон: (383) 265–87–59.
Для детей от 13 до 16 лет.
10. Керлинг
Спортивная школа «Центр зимних видов спорта».
- адрес: ул. Станционная, д. 102;
- телефон: (383) 285–56–66.
Для детей от 8 до 18 лет.
В разделе физкультурно-спортивного направления много приглашений на художественную гимнастику
Фото: Александр Ощепков
Поделиться
11. Художественная гимнастика
Детско-юношеский (физкультурный) центр № 1 «ЛИГР».
- адрес: ул. Кропоткина, д. 110, ул. Союза Молодежи, д. 10, ул. Тимирязева, д. 81а;
- телефон: (383) 225–27–71.
Для детей от 5 до 18 лет.
12. Бокс
Детско-юношеский (физкультурный) центр № 1 «ЛИГР».
- адрес: ул. Аэропорт, д. 21/1;
- телефон: (383) 225–27–71.
Для детей от 9 до 15 лет.
13. Первоначальная авиационная подготовка на планере
Сибирский авиационный кадетский корпус им. А. И. Покрышкина (школа-интернат).
- адрес: ул. Урманова, 18;
- телефон: (383) 209–35–20.
Для детей от 12 до 13 лет.
14. Каратэ
Детско-юношеский (физкультурный) центр № 1 «ЛИГР».
- адрес: ул. Олеко Дундича, д. 1/1;
- телефон: (383) 225–27–71.
Для детей от 8 до 18 лет.
15. Хоккей
Детско-юношеский (физкультурный) центр № 1 «ЛИГР».
- адрес: ул. Достоевского, д. 27;
- телефон: (383) 225–27–71.
Для детей от 8 до 18 лет.
В основном здесь предложения танцев от бальных до народных направлений, а также множество секций по рисованию, пению и игре на различных музыкальных инструментах.
Много организаций зовут детей учиться рисованию
Фото: Александр Ощепков
Поделиться
1. Спортивно-бальные танцы
Центр внешкольной работы «Галактика».
- адрес: ул. Липецкая, д. 25/2;
- телефон: (383) 279–75–73.
Для детей от 5 до 18 лет.
2. Парикмахерское искусство
Детский (подростковый) центр «Юность».
- адрес: ул. Красных Зорь, д. 1;
- телефон: (383) 274–01–41.
Занятия проводятся 2 раза в неделю. Для детей от 12 до 16 лет.
3. Песочная анимация
Центр детского творчества «Содружество».
- адрес: ул. 25 лет Октября, 16/3;
- телефон: (383) 265–87–59.

Для детей от 7 до 9 лет.
4. Картины из соломки
Центр детского творчества «Содружество».
- адрес: ул. 25 лет Октября, 16/3;
- телефон: (383) 265–87–59.
Для детей от 8 до 18 лет.
5. Графический дизайн
Центр детского творчества Советского района.
- адрес: ул. Приморская, д. 3;
- телефон: (383) 330–25–71.
Для детей от 11 до 16 лет.
Многие кружки предлагают разные группы на выбор
Фото: Катерина Калиневич
Поделиться
6. Документальное и научно-популярное кино
Детско-юношеский центр «Старая мельница».
- адрес: ул. Орджоникидзе, д. 37;
- телефон: (383) 222–53–59.
Для детей от 10 до 17 лет.
7. Брейкданс
Детский (подростковый) центр «Юность».
- адрес: ул. Объединения, д.
 23/2;
23/2; - телефон: (383) 274–01–41.
Для детей от 5 до 13,5 лет.
8. Ювелирное искусство
Детская школа искусств «Весна».
- адрес: ул. Лермонтова, д. 45;
- телефон: (383) 224–89–01.
Для детей от 14 до 18 лет.
9. Театр кукол
Детская школа искусств «Весна».
- адрес: ул. Лермонтова, д. 45;
- телефон: (383) 224–89–01.
Для детей от 6,5 до 12 лет.
10. Лепка из глины
Центр дополнительного образования «Алые паруса».
- адрес: ул. 1905 года, д. 12;
- телефон: (383) 221–19–55.
Для детей от 6 до 15 лет.
11. Выжигание по ткани
Центр детского творчества «Содружество».
- адрес: ул. 25 лет Октября, 27;
- телефон: (383) 265–87–59.
Для детей от 9 до 16 лет.
12. Моделирование одежды
Детский (подростковый) центр «Юность».
- адрес: ул. Объединения, д. 23/2;
- телефон: (383) 274–01–41.
Для детей от 7 до 18 лет.
В этом направлении можно найти кружки и секций для детей, которые интересуются историей своего родного края, любят походы и очень не хотят сидеть на месте.
Туризм тоже требует подготовки
Фото: Александр Ощепков
Поделиться
1. Изучение микромира в микроскопе
Центр детского творчества Советского района.
- адрес: ул. Приморская, д. 3;
- телефон: (383) 330–25–71.
Для детей от 10 до 14 лет.
2. Школа юного кинолога
Центр детского творчества «Содружество».
- адрес: ул. Рассветная, д. 2а;
- телефон: (383) 265–87–59.
Занятия проводятся 2 раза в неделю. Для детей от 7 до 18 лет.
3. Экоклуб Formica
Дворец творчества детей и учащейся молодежи «Юниор».
- адрес: ул. Ученых, д. 10;
- телефон: (383) 217–86–87.
Занятия проводятся 2 раза в неделю. Для детей от 9 до 14 лет.
4. Школа выживания. Сибирский маршрут
Центр внешкольной работы «Галактика».
- адрес: пр. Дзержинского, д. 83;
- телефон: (383) 279–75–73.
Для детей от 10 до 17 лет.
5. Юный спасатель
Центр детского творчества «Содружество».
- адрес: ул. Народная, д. 11;
- телефон: (383) 265–87–59.
Для детей от 14 до 18 лет.
6. Краеведение
Центр дополнительного образования «Лад».
- адрес: ул. Пихтовая, д. 44;
- телефон: (383) 338–84–57.
Для детей от 7 до 12 лет.
В этом разделе есть кружки и секции практически по любому современному направлению, связанному с моделированием, компьютерными технологиями, конструкторским делом.
Компьютерные технологии сейчас особенно востребованы
org/Person»>Фото: Ольга Бурлакова
Поделиться
1. Морское многоборье
Детский морской центр «Флагман».
- адрес: ул. Большевистская, д. 175/6;
- телефон: (383) 240–80–65.
Для детей от 7 до 16 лет.
2. Основы робототехники
Дом детского творчества «Центральный».
- адрес: Каменская, д. 82;
- телефон: (383) 201–17–44.
Занятия проводятся раз в неделю. Для детей от 7 до 10 лет.
3. Управление парусной яхтой
Детский морской центр «Флагман».
- адрес: ул. Большевистская, д. 175/6;
- телефон: (383) 240–80–65.
Для детей от 5 до 18 лет.
4. Авиамоделирование
Дворец творчества детей и учащейся молодежи «Юниор».
- адрес: ул.Кирова, д. 44/1
- телефон: (383) 217–86–87.
Для детей от 10 до 17 лет.
5. 3D моделирование 3D-ручкой
Центр дополнительного образования «Лад».
- адрес: ул. Ученическая, д. 5
- телефон: (383) 338–84–57.
Для детей от 10 до 15 лет.
6. Компьютерная графика и анимация
Дом детского творчества «Центральный».
- адрес: ул. Крылова, д. 38;
- телефон: (383) 201–17–44.
Занятия проводятся раз в неделю. Для детей от 7 до 11 лет.
Дети могут выбрать самые разные направления
Фото: Ольга Бурлакова
Поделиться
7. Начальное техническое конструирование
Центр дополнительного образования «Алые паруса».
- адрес: ул. 1905 года, д. 12;
- телефон: (383) 221–19–55.
Занятия проводятся раз в неделю. Для детей от 5 до 14 лет.
8. Снайперская стрельба
Центр дополнительного образования «Алые паруса».
- адрес: ул. 1905 года, д. 12, ул. Советская, д. 93;
- телефон: (383) 221–19–55.
Занятия проводятся раз в неделю. Для детей от 10 до 17 лет.
9. Радиотехника
Дом детского творчества им. А.И.Ефремова.
- адрес: ул. Мира, д. 36;
- телефон: (383) 353–45–86.
Для детей от 10 до 18 лет.
10. Юный автомеханик
Областной центр детского (юношеского) технического творчества «Автомотоцентр».
- адрес: ул. Юннатов, д. 72;
- телефон: (383) 226–04–29.
Занятия проводятся 3 раза в неделю. Для детей от 10 до 18 лет.
11. Стендовое моделирование исторических миниатюр
Центр детского творчества «Содружество».
- адрес: МБОУ СОШ №105;
- телефон: (383) 265–87–59.
Для детей от 9 до 18 лет.
12. Мотоспорт
Областной центр детского (юношеского) технического творчества «Автомотоцентр».
- адрес: ул. Юннатов, д. 72;
- телефон: (383) 226–04–29.
Для детей от 8 до 18 лет.
13. Экспериментальное судостроение
Детский морской центр «Каравелла» им. А.Москаленко.
- адрес: ул. Вяземская, д. 4;
- телефон: (383) 276–35–31.
Для детей от 10 до 17 лет.
Web-дизайн тоже сейчас очень востребован
Фото: Александр Ощепков
Поделиться
14. Мультипликация
Центр дополнительного образования «Алые паруса».
- адрес: ул. Советская, д. 93;
- телефон: (383) 221–19–55.
Для детей от 9 до 12 лет.
15. Столярное дело
Центр дополнительного образования «Алые паруса».
- адрес: ул. 1905 года, д. 12;
- телефон: (383) 221–19–55.
Для детей от 9 до 17 лет.
16. Картинг
Областной центр детского (юношеского) технического творчества «Автомотоцентр».
- адрес: ул. Юннатов, д. 72;
- телефон: (383) 226–04–29.

Для детей от 6 до 18 лет.
17. Web-дизайн
Дворец творчества детей и учащейся молодежи «Юниор».
- адрес: ул.Кирова, д. 44/1
- телефон: (383) 217–86–87.
Для детей от 11 до 18 лет.
В этом году 86 выпускников в Новосибирской области сдали ЕГЭ на 100 баллов. Двое из них получили максимальную оценку сразу по двум предметам. Корреспондент НГС узнала, в каких школах учатся самые умные выпускники.
А вот история сибирячки, которая тратит по 40 тысяч в месяц на репетиторов для дочки. Почитайте, зачем она это делает.
Интересна и история сына футболиста, который бросил спорт и стал мультистобалльником (он признался, кем на самом деле хочет стать и сколько планирует зарабатывать).
частей круга — определение, формулы, примеры
Есть много частей круга , которые делают его кругом. Круг представляет собой двумерную форму и измеряется с точки зрения его радиуса. Слово «круг» происходит от греческого слова «киркос», означающего «кольцо» или «обруч». К частям круга относятся радиус, диаметр, длина окружности и так далее. Давайте узнаем о круге и его частях подробно.
К частям круга относятся радиус, диаметр, длина окружности и так далее. Давайте узнаем о круге и его частях подробно.
| 1. | Определение круга |
| 2. | Из каких частей состоит круг? |
| 3. | Часто задаваемые вопросы о частях круга |
Определение круга
Окружность можно определить как двухмерную фигуру, образованную набором точек, смежных друг с другом и равноудаленных от фиксированной точки. Неподвижная точка на этой изогнутой плоской фигуре называется центром окружности, общее расстояние между точками от центра называется радиусом, а линия, пересекающая центр окружности, начинающаяся из одной точки в другую, называется диаметр. Круг имеет две основные области, а именно: внутреннюю часть круга и внешнюю часть круга. Внутренняя часть круга состоит из области внутри круга, а внешняя часть круга — это область вне круга.
Из каких частей состоит круг?
Круг — это замкнутая фигура с изогнутой границей, состоящая из множества частей, представляющих свойства и характеристики круга.
Круг и его части
Различные части круга перечислены ниже:
- Окружность
- Радиус
- Диаметр
- Аккорд
- Касательная
- Секущая
- Арка
- Сегмент
- Сектор
Давайте подробно обсудим каждую из частей.
Окружность круга
Окружность круга является его границей. Другими словами, когда мы измеряем границу или расстояние вокруг круга, эта мера называется окружностью и выражается в единицах длины, таких как сантиметры, метры или километры. Окружность круга состоит из трех наиболее важных элементов, а именно центра, диаметра и радиуса.
Поскольку мы не можем использовать линейку (шкалу) для измерения расстояния до этой изогнутой фигуры, мы применяем формулу, в которой используются радиус, диаметр и значение числа Пи (π).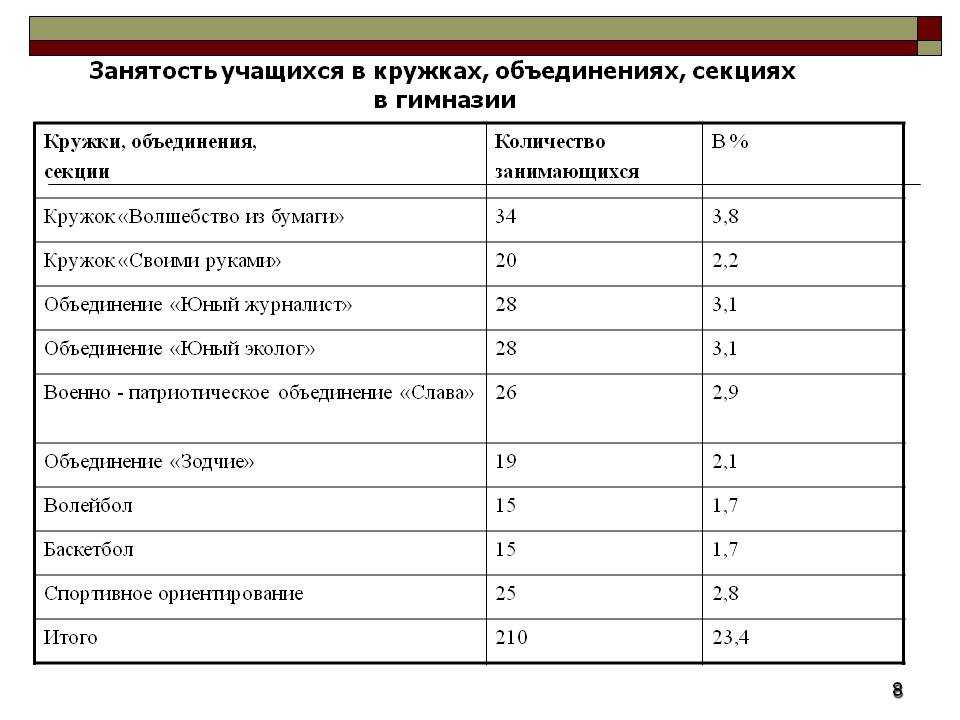 Формулы для длины окружности даются следующим образом:
Формулы для длины окружности даются следующим образом:
- Когда радиус дан: Длина окружности по формуле = 2πr
- Если задан диаметр: длина окружности по формуле = π × D
Где,
- r = радиус окружности.
- D = диаметр окружности.
- π = Пи со значением, приближенным к 3,14159 или 22/7.
Радиус окружности
Радиус окружности — это длина отрезка, соединяющего центр окружности с любой точкой окружности. У круга может быть много радиусов (форма множественного числа радиуса), и они измеряются одинаково. Обычно радиус окружности обозначают буквой «r».
Для вычисления радиуса круга, когда известны диаметр, площадь круга и длина окружности, мы используем следующие формулы:
- Радиус окружности = Диаметр / 2. Диаметр в два раза больше длины радиуса, а также является самой длинной хордой окружности. Когда диаметр известен, мы используем эту формулу.
- Радиус окружности = Окружность / 2π — Окружность — это периметр круга, и когда длина окружности задана, мы используем эту формулу.

- Радиус круга = √(Площадь/π) – Площадь круга – это пространство внутри круга. Следовательно, когда дана площадь круга, мы используем эту формулу.
Диаметр окружности
Диаметр окружности — это отрезок, который проходит через центр окружности и имеет конечные точки, лежащие на окружности окружности. Диаметр также известен как самая длинная хорда круга и в два раза больше длины радиуса. Диаметр измеряется от одного конца круга до точки на другом конце круга, проходящей через центр. Диаметр обозначается буквой D. Может быть бесконечное количество диаметров, где длина каждого диаметра окружности равна длине.
Чтобы вычислить диаметр круга, когда известны радиус, площадь круга и длина окружности, мы используем следующие формулы:
- Диаметр = длина окружности/π (используется, когда дана длина окружности)
- Диаметр = Радиус × 2 (используется, когда указан радиус)
- Диаметр = 2√(Площадь/π) (используется, когда дана площадь круга)
Хорда окружности
Хорда окружности — это отрезок, соединяющий две точки на окружности окружности. Хорда делит круг на две области, известные как сегмент круга, который можно назвать второстепенным сегментом и большим сегментом в зависимости от области, охватываемой хордой. В круге, когда хорда бесконечно продолжена в обе стороны, она становится секущей. На приведенном ниже рисунке PQ представлен хордой окружности с центром O в центре.
Хорда делит круг на две области, известные как сегмент круга, который можно назвать второстепенным сегментом и большим сегментом в зависимости от области, охватываемой хордой. В круге, когда хорда бесконечно продолжена в обе стороны, она становится секущей. На приведенном ниже рисунке PQ представлен хордой окружности с центром O в центре.
Чтобы вычислить хорду окружности, мы используем две основные формулы:
- Длина хорды = 2 × √(r 2 − d 2 ) (используя перпендикулярное расстояние от центра)
- Длина хорды = 2 × r × sin(c/2) (с использованием тригонометрии)
Где,
- r — радиус окружности
- c — угол, образуемый в центре хордой
- d — расстояние по перпендикуляру от хорды до центра окружности.
.
Касательная окружности
Касательная окружности определяется как прямая линия, которая касается кривой окружности только в одной точке и не входит внутрь окружности. Касательная касается радиуса окружности под прямым углом. Два основных аспекта, которые следует помнить в касательной, — это наклон (м) и точка на линии. Общее уравнение или формула касательной к окружности:
Касательная касается радиуса окружности под прямым углом. Два основных аспекта, которые следует помнить в касательной, — это наклон (м) и точка на линии. Общее уравнение или формула касательной к окружности:
- Уравнение касательной к окружности x 2 + y 2 = a 2 для линии y = mx + c задается уравнением y = mx ± a √[1+ m 2 ]
- TANGENTS TO CIRCLE Уравнение x 2 + Y 2 = A 2 AT (A 1 , B 1) IS XA 1 + YB 1 = A 1 + YB 1 = A . Это означает, что уравнение касательной выражается как xa 1 + yb 1 = a 2 , где a 1 и b 1 — координаты, в которых проведена касательная.
Секущая окружности
Секущая окружности — это линия, пересекающая окружность и пересекающая окружность в двух различных точках. Разница между хордой и секущей заключается в том, что хорда — это отрезок, концы которого находятся на окружности окружности, тогда как секущая проходит через окружность, образуя хорду или диаметр окружности.
В круге используются три теоремы о секущих, которые приведены ниже:
- Теорема 1: Когда две секущие пересекаются во внешней точке, произведение одного целого секущего и его внешнего сегмента равно произведению другого целого секущего и его внешнего сегмента.
- Теорема 2: Две секущие могут пересекаться внутри или вне круга.
- Теорема 3: Если секущая и касательная проведены к окружности из общей внешней точки, то произведение длины всей секущей и ее внешней секущей равно квадрату длины касательной.
На приведенном ниже рисунке показаны секущая PQ и хорда AB.
Дуга окружности
Дуга окружности представляет собой изогнутую часть или часть окружности окружности. Другими словами, изогнутая часть объекта математически называется дугой. Дуга окружности имеет две дуги, а именно малую дугу и большую дугу. Чтобы найти меру этих дуг, нам нужно найти длину дуги вместе с углом, подвешенным на дуге любых двух точек. Для расчета длины дуги мы используем различные формулы, основанные на единицах измерения центрального угла (градусы или радианы).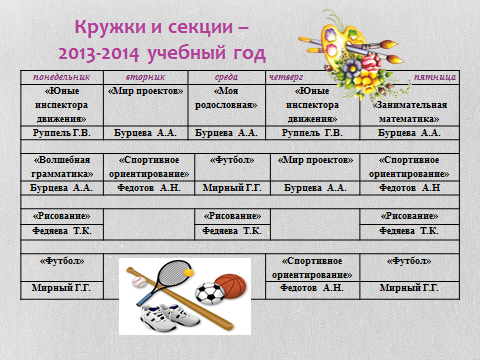 Для круга формула длины дуги равна θ, умноженному на радиус круга. Формулы:
Для круга формула длины дуги равна θ, умноженному на радиус круга. Формулы:
- Длина дуги = θ × r (используется для радианов)
- Длина дуги = θ × (π/180) × r (используется для градусов)
Где,
- L = длина дуги
- θ = центральный угол дуги
- r = радиус окружности
Сегмент окружности
Сегмент окружности — это область, ограниченная дугой и хордой окружности. Сегменты бывают двух типов — малый сегмент и большой сегмент. Малый сегмент образован малой дугой, а большой сегмент образован большой дугой окружности. Чтобы вычислить отрезок круга, мы рассматриваем площадь отрезка, состоящего из сектора (дуга + 2 радиуса) и треугольника. Следовательно, формула площади сегмента может быть выражена следующим образом
- Площадь сегмента круга = площадь сектора — площадь треугольника
Примечание: Чтобы найти площадь большого сегмента круга, мы просто вычитаем соответствующую площадь меньшего сегмента из общей площади круга.
Сектор круга
Сектор круга представляет собой круговую часть круга, состоящую из дуги с двумя радиусами, делящими круг на меньший сектор и большой сектор. Большая часть круга называется большим сектором, тогда как меньшая часть круга называется малым сектором. 2 радиуса встречаются в части окружности круга, известной как дуга, образуя сектор круга. Формулы для расчета сектора круга:
- Площадь сектора (A) = (θ/360°) × πr 2 (когда задан угол)
- Длина секции (l) = (θπr)/180 (если указана длина)
- Площадь сектора круга = (l × r)/2 (если заданы длина и радиус)
- Периметр сектора круга = 2 Радиус + ((θ/360) × 2πr )
Где,
- r = радиус окружности.
- l = длина дуги.
- θ = угол в градусах.
- π = Пи со значением, приближенным к 3,14159 или 22/7.
☛ Похожие темы
- Окружность к диаметру
- Полукруг
- 3D-фигуры
Часто задаваемые вопросы о частях круга
Из каких частей состоит круг?
К частям окружности относятся длина окружности, радиус, диаметр, хорда, касательная, секущая, дуга, сегмент и сектор. Каждая из этих частей круга играет важную роль в формировании круга.
Каждая из этих частей круга играет важную роль в формировании круга.
Какая часть круга самая длинная?
Самая длинная часть круга — это диаметр, т. е. расстояние от одного конца круга до другого конца круга. Отрезок, проходящий через центр, соединяющий две точки окружности, считается самой длинной частью. Следует отметить, что диаметр является самой длинной хордой окружности.
Каковы 4 основные части круга?
Четыре основные части круга: радиус, диаметр, центр и окружность. Центр окружности – это точка, равноудаленная от всех сторон окружности. Радиус — это длина линии от центра окружности до любой точки кривой окружности. Диаметр – это отрезок, который пересекает центр круга от одного конца круга до другого конца. Окружность круга — это граница или расстояние, которое завершает круг.
На сколько частей делится отрезок окружности?
Сегмент круга делится на две части — малый сегмент и большой сегмент. Меньшая часть сегмента круга называется малым сегментом, тогда как большая часть сегмента круга называется большим сегментом.
Что такое центр круга?
Центр окружности — это точка внутри окружности, равноудаленная от всех точек на кривой окружности. Центр круга также помогает в создании круга по любому измерению.
Что такое секущие в круге?
Сеанс окружности — это линия, пересекающая окружность и пересекающая окружность в двух различных точках. Разница между хордой и секущей заключается в том, что хорда — это отрезок, концы которого находятся на криволинейной части окружности, тогда как секущая проходит через окружность, образуя хорду или диаметр окружности.
Конические сечения (парабола, эллипс, гипербола, окружность)
Конические сечения являются одной из важных тем в геометрии. В математике существуют различные типы конических сечений, которые можно определить на основе угла, образованного между плоскостью и пересечением с ней прямого кругового конуса.
Содержание:
- Определение
- Формулы
- Эксцентриситет фокуса и директриса
- Параметры
- Секции конуса
- Круг
- Эллипс
- Парабола
- Гипербола
- Стандартная форма
- Примеры
- Уравнения
- Решенные вопросы
- Практические вопросы
- Часто задаваемые вопросы
Что такое конические сечения
Кривая, образованная пересечением прямого кругового конуса с плоскостью, называется «конической» .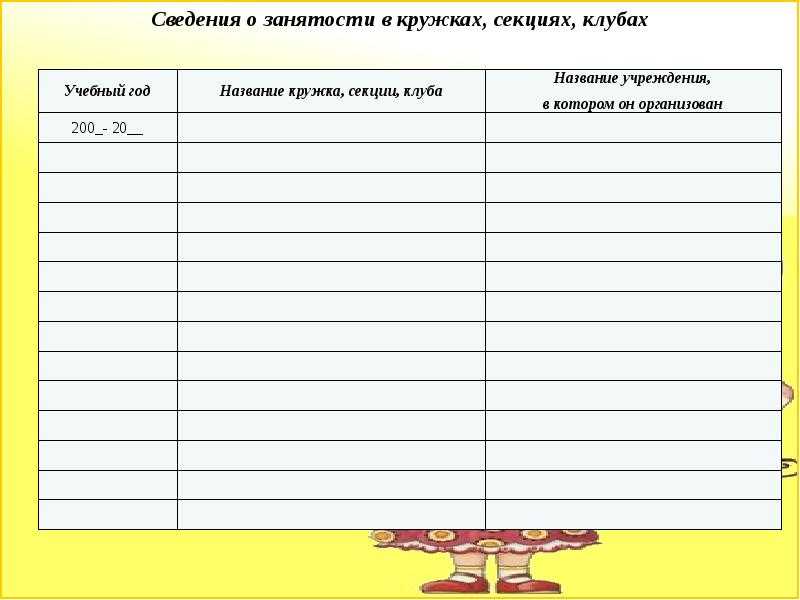 Он имеет выдающиеся свойства в евклидовой геометрии. Вершина конуса делит его на два покрова, называемых верхним покровом и нижним покровом.
Он имеет выдающиеся свойства в евклидовой геометрии. Вершина конуса делит его на два покрова, называемых верхним покровом и нижним покровом.
На рисунке B конус пересекается плоскостью, и полученное сечение называется коническим сечением. В зависимости от положения плоскости, пересекающей конус, и угла пересечения β получаются различные типы конических сечений. А именно;
- Круг
- Эллипс
- Парабола
- Гипербола
Задние зеркала, которые вы видите в своей машине, или огромные круглые серебряные зеркала, которые вы видите на станции метро, являются примерами кривых. Кривые имеют огромное применение повсюду, будь то изучение движения планет, проектирование телескопов, спутников, рефлекторов и т. д. Конические состоят из кривых, которые получаются при пересечении плоскости с прямым круговым конусом с двойной вершиной. О конических сечениях в 11-м классе было широко объяснено. Давайте обсудим образование различных сечений конуса, формулы и их значение.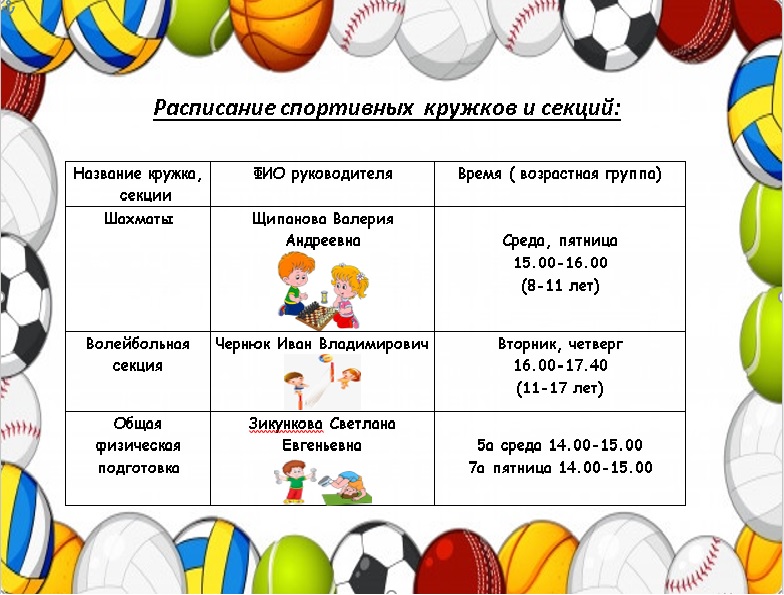
Формулы конического сечения
Проверьте формулы для различных типов сечений конуса в таблице, приведенной здесь.
| Круг | (х-а) 2 +(у-б) 2 =r 2 | Центр (a,b) Радиус r |
| Эллипс с горизонтальной большой осью | (x−a) 2 /h 2 +(y−b) 2 /k 2 =1 | Центр (а, б) Длина большой оси – 2h. Длина малой оси – 2k. Расстояние между центром и любым фокусом равно c с c 2 =h 2 −k 2 , h>k>0 |
| Эллипс с вертикальной большой осью | (x−a) 2 /k 2 +(y−b) 2 /h 2 =1 | Центр (a, b) Длина большой оси 2h. Длина малой оси – 2k. Расстояние между центром и любым фокусом равно c с c 2 =h 2 −k 2 , h>k>0 |
| Гипербола с горизонтальной поперечной осью | (x-a) 2 /h 2 -(y-b) 2 /k 2 =1 | Центр (a,b) Расстояние между вершинами 2h Расстояние между фокусами 2k. 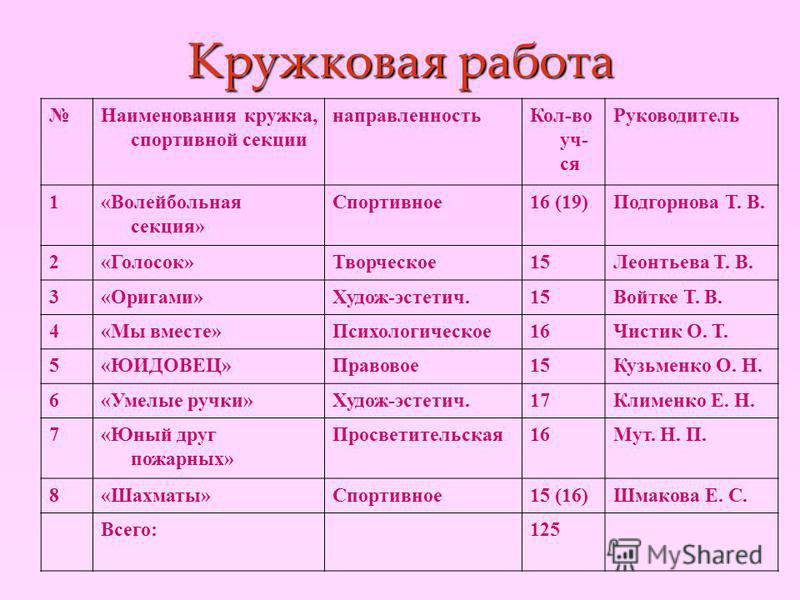 с 2 =ч 2 + к 2 |
| Гипербола с вертикальной поперечной осью | (х-а) 2 /k 2 −(y−b) 2 /h 2 =1 | Центр (a,b) Расстояние между вершинами 2h Расстояние между фокусами 2k. с 2 = ч 2 + к 2 |
| Парабола с горизонтальной осью | (y−b) 2 =4p(x−a), p≠0 | Вершина (a,b) Фокус (a+p,b) Директриса – линия x=a−p Ось – линия y=b |
| Парабола с вертикальной осью | (x−a) 2 =4p(y−b), p≠0 | Вершина (a,b) Фокус (a+p,b) Директриса – линия x=b−p Ось – линия x=a |
Фокус, эксцентриситет и направляющая конуса
Коническое сечение также может быть описано как геометрическое место точки P, движущейся в плоскости фиксированной точки F, известной как фокус (F) , и фиксированной линии d, известной как направляющая (с фокусом не на d) таким образом, что отношение расстояния точки P от фокуса F к ее расстоянию от d равно константе e, известной как эксцентриситет .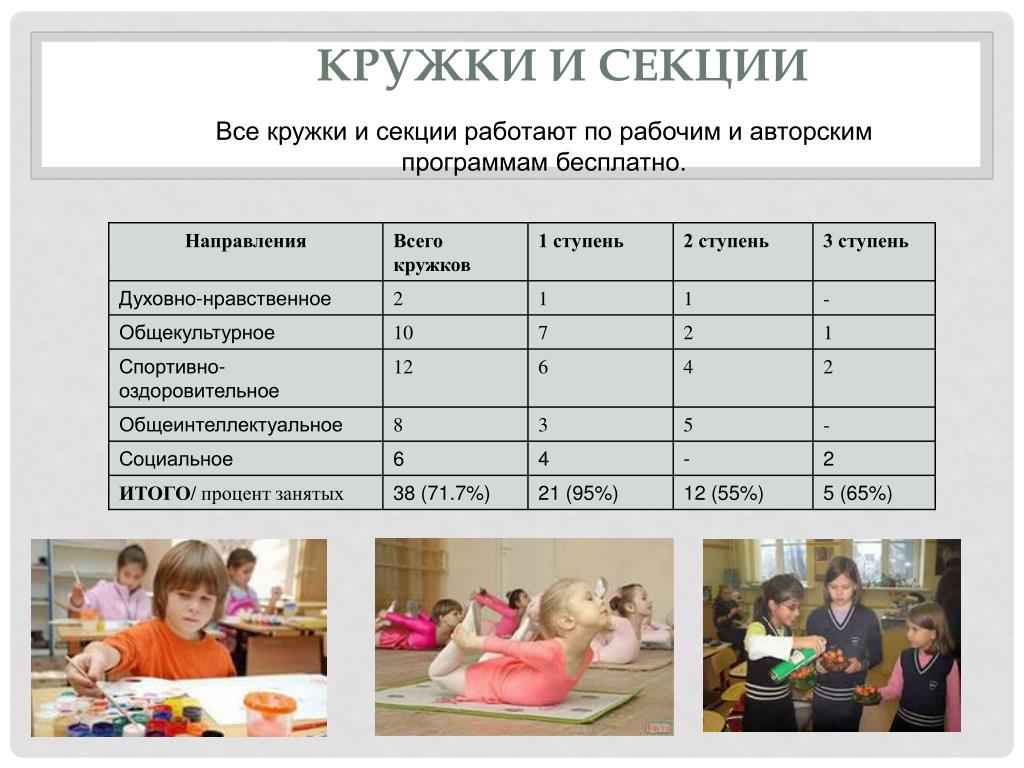 Сейчас
Сейчас
- Если эксцентриситет e = 0, коника представляет собой окружность
- Если 0
- Если e=1, коника является параболой
- А если e>1, то это гипербола
Итак, эксцентриситет является мерой отклонения эллипса от окружности. Предположим, угол, образованный между поверхностью конуса и его осью, равен β, а угол, образованный между секущей плоскостью и осью, равен α, эксцентриситет равен;
e = cos α/cos β
Параметры Conic
Помимо фокуса, эксцентриситета и директрисы, есть еще несколько параметров, определенных для конических сечений.
- Главная ось: Линия, соединяющая две фокальные точки или фокусы эллипса или гиперболы. Его середина является центром кривой.
- Линейный эксцентриситет: Расстояние между фокусом и центром сечения.
- Latus Rectum: Хорда сечения, параллельная директрисе, проходящая через фокус.

- Фокус Параметр: Расстояние от фокуса до соответствующей директрисы.
- Большая ось: Хорда, соединяющая две вершины. Это самая длинная хорда эллипса.
- Малая ось: Кратчайшая хорда эллипса.
Также читайте:
Секции конуса
Рассмотрим фиксированную вертикальную линию «l» и другую линию «m», наклоненную под углом «α», пересекающую «l» в точке V, как показано ниже:
Инициалы, упомянутые на приведенном выше рисунке А, имеют следующие значения:
- V — вершина конуса
- l — ось конуса
- м, вращающаяся линия образующая конуса
Кратко обсудим различные конические сечения, образующиеся при пересечении плоскостью покровов (исключая вершину).
Круг конического сечения
Если β=90 o , сформированное коническое сечение представляет собой круг, как показано ниже.
Эллипс конического сечения
Если α<β<90 o , образованное таким образом коническое сечение представляет собой эллипс, как показано на рисунке ниже.
Парабола конического сечения
Если α=β, сформированное коническое сечение представляет собой параболу (представленную оранжевой кривой), как показано ниже.
Гипербола конического сечения
Если 0≤β<α, то плоскость пересекает оба покрова, и образованное таким образом коническое сечение известно как гипербола (обозначена оранжевыми кривыми).
Видео урок
Визуализация конических сечений
Стандартные формы конических сечений
После введения декартовых координат свойство focus-directrix можно использовать для записи уравнений, представленных точками конического сечения. Когда координаты изменяются вместе с вращением и перемещением осей, мы можем привести эти уравнения к стандартным формам. Для эллипсов и гипербол стандартная форма имеет ось x в качестве главной оси и начало координат (0,0) в качестве центра. Вершины (±a, 0) и фокусы (±c, 0). Определим b уравнениями c 2 = a 2 − b 2 для эллипса и c 2 = a 2 + b 2 для гиперболы.
Для эллипсов и гипербол стандартная форма имеет ось x в качестве главной оси и начало координат (0,0) в качестве центра. Вершины (±a, 0) и фокусы (±c, 0). Определим b уравнениями c 2 = a 2 − b 2 для эллипса и c 2 = a 2 + b 2 для гиперболы.
Для круга c = 0, поэтому a 2 = b 2 . Для параболы стандартная форма имеет фокус на оси x в точке (a, 0), а направляющая — это линия с уравнением x = -a. В стандартной форме парабола всегда проходит через начало координат.
- Круг: x 2 +y 2 =a 2
- Эллипс: x 2 /a 2 + y 2 /b 2 = 1
- Гипербола: x 2 /a 2 – y 2 /b 2 = 1
- Парабола: y 2 =4ax, когда a>0
Примеры конических сечений
Если плоскость пересекает точно в вершине конуса, могут возникнуть следующие случаи:
- Если α< β≤90 ° , то плоскость пересекает вершину точно в точке.

- Если α=β, то плоскость при пересечении с конусом образует прямую, содержащую образующую конуса. Это условие является вырожденной формой параболы.
- Если 0≤β<α, то образующееся сечение представляет собой пару пересекающихся прямых. Это условие является вырожденной формой гиперболы.
Уравнения конических сечений
| Коническое сечение Название | Уравнение, когда центр находится в начале координат, т. е. (0, 0) | Уравнение, когда центр равен (h, k) |
| Круг | x 2 + y 2 = r 2 ; r — радиус | (x – h) 2 + (y – k) 2 = r 2 ; r — радиус |
| Эллипс | (х 2 /а 2 ) + (у 2 /б 2 ) = 1 | (x – h) 2 /a 2 + (y – k) 2 /b 2 = 1 |
| Гипербола | (х 2 /а 2 ) – (у 2 /б 2 ) = 1 | (x – h) 2 /a 2 – (y – k) 2 /b 2 = 1 |
| Парабола | y 2 = 4ax, где a — расстояние от начала координат до фокуса | |
Решенные вопросы по коническим сечениям
Вопрос 1:
Найти координаты фокуса и вершины, уравнения направляющей и оси, длину прямой прямой параболы y 2 = 8x.
Решение:
Сравнивая данное уравнение параболы со стандартной формой y 2 = 4ax, получаем a = 2. Таким образом,
| Координаты фокуса | F(a, 0), то есть F(2, 0) |
| Координаты вершины | О(0, 0) |
| Уравнение Директрисы | х = –а, то есть х = –2 |
| Уравнение оси | Его осью является ось x, уравнение которой y = 0 |
| Длина широкой прямой кишки | 4а, то есть 4×2 = 8 единиц |
Вопрос 2:
Дан эллипс, фокусы которого находятся в точке (±4, 0), а эксцентриситет равен ⅓. Найдите уравнение эллипса.
Решение:
По координатам фокуса получаем, что эллипс является горизонтальным эллипсом, большая ось которого лежит на оси x.
Пусть уравнение эллипса будет
x 2 /a 2 + y 2 /b 2 = 1, где a 2 > b 2
Для эллипса эксцентриситет e = c/a ⇒ a = c/a ⇒ a = c/a ⇒ a = c/e ±c, 0) — фокус
∴ a = 4/(⅓ ) = 12.
Теперь c 2 = (a 2 – b 2 )
⇒ 13 b 2991 a 2 – c 2 ) = 12 2 – 4 2 = 128
Следовательно, уравнение эллипса
x 2 y/1940134 2 /128 = 1.
Вопрос 3:
Для данной гиперболы x 2 /36 – y 2 /64 = 1. Найдите следующее:
x
оси ;
(ii) координаты вершин и фокусов;
(iii) эксцентриситет;
(iv) длина широкой прямой кишки.
Решение:
Сравнение данного уравнения гиперболы со стандартным уравнением x 2 /a 2 – y 2 /b 2 = 1, получаем a 2 = 36 и b 2 = 64.
∴ a = 6, b = 8 и c = (a 2 + b 5 2 ) ½ = (36 + 64) ½ = 10.
| Длина осей | Длина поперечной оси = 2a = 12 единиц Длина сопряженной оси = 2b = 16 единиц |
| Координаты вершин | A(-a, 0) и B(a, 0), то есть A(-6, 0) и B(6, 0) |
| Координаты очагов | F 1 (-c, 0) и F 2 (c, 0), то есть F 1 (-10, 0) и F 2 (10, 0) |
| Эксцентриситет | е = с/а = 10/6 = 5/3 |
| Длина широкой прямой кишки | 2b 2 /a = (2 × 8 2 )/6 = 64/3 единиц |
Практические вопросы
- Если гипербола имеет вершины в точках (±2, 0) и фокусы в точках (±3, 0).
 Найдите уравнение гиперболы.
Найдите уравнение гиперболы. - Найти координаты фокуса и вершины, уравнения директрисы и оси и длину широкой прямой кишки параболы x 2 = –16y.
- Найти координаты фокусов и вершин, длины большой и малой осей, эксцентриситет и длину широкой прямой кишки эллипса: x 2 /16 + y 2 /9 = 1.
Загрузите BYJU’S-The Learning App и получите персонализированные видеоролики, в которых концепции геометрии объясняются с помощью интерактивных видеороликов.
Часто задаваемые вопросы о конических сечениях
Что такое 4 конических сечения?
В зависимости от наклона угла между плоскостью и конусом конические сечения можно разделить на 4 типа. Это:
Окружности
Эллипсы
Параболы
Гиперболы
Что такое коническое сечение в реальной жизни?
Мы можем наблюдать конические сечения во многих реальных ситуациях. Например, когда мы рассматриваем Солнце как один фокус, то пути планет образуют вокруг него эллипсы.