Как выбрать кружки и секции — Школа.Москва

УЧИМСЯ ВСЕЙ СЕМЬЕЙ!

Занятия по интересам для каждого ребенка

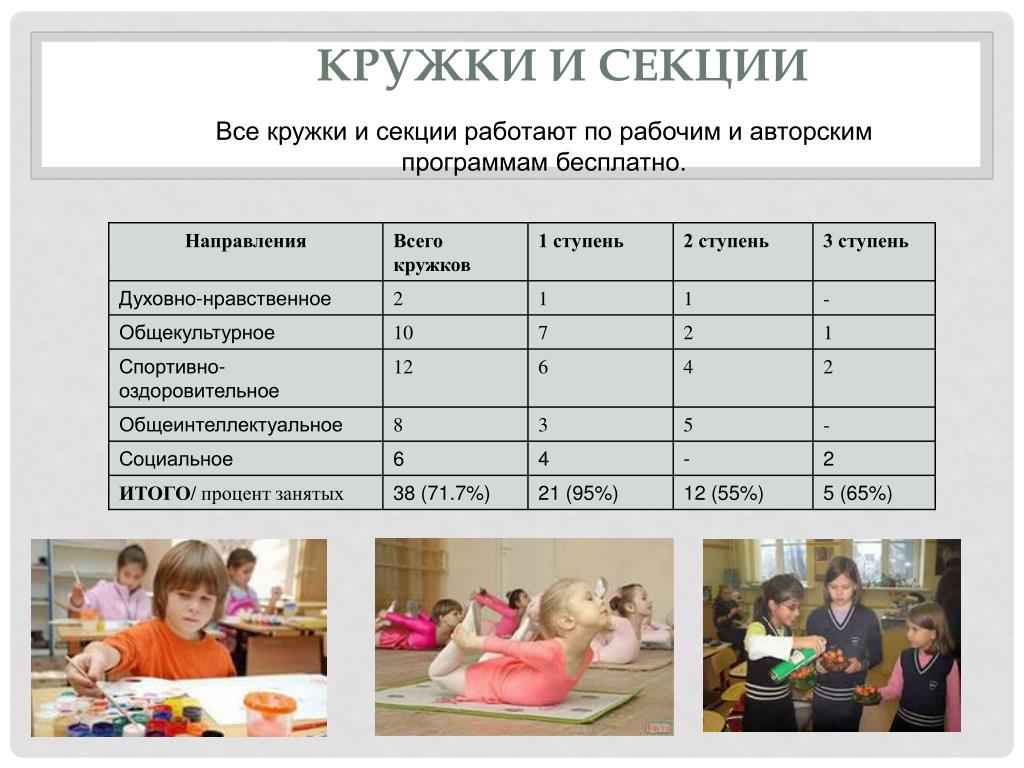
В школах, колледжах, вузах и организациях дополнительного образования, подведомственных Департаменту образования и науки города Москвы, открыто более 130 тысяч кружков и секций.

Можно выбрать дополнительное образование на любой вкус и интерес:

• техническое направление,
• естественные науки,
• физкультура и спорт,
• искусство и творчество,
• туристско-краеведческая направленность,
• социально-гуманитарная сфера.

Кружки можно посещать в удобное время — утром, днем или вечером.

Эстафета талантов «Что можешь ты?»

5 декабря 2022 стартует эстафета талантов
«Что можешь ты?»!

• Ты занимаешься в кружках и секциях в школе или в городских центрах творчества?
• Ты научился там круто танцевать, рассказывать стихи, петь, показывать фокусы или что-то еще?
• Тогда эта эстафета — для тебя!

Запиши короткий видеоролик о том, что ты умеешь делать, в чем твой талант, присылай его в форму обратной связи или выкладывай в соцсетях с хештегом #ЧтоМожешьТы?

Самые интересные ролики мы покажем в соцсетях Департамента образования и науки города Москвы, а самых выдающихся талантов Московский образовательный канал пригласит на профессиональные съемки!

Прислать видео

Смотреть видео «Что можешь ты?»

• Яков Прокофьев, капитан команды по гандболу

  Яков из школы № 188 занимается в секции гандбола ДЮСШ «Воробьевы горы» Московского дворца пионеров. ..

• Георгий Трусов, юный химик

  Георгий, ученик школы № 192, уже умеет проводить сложные химические опыты и владеет методами…

• Таисия Зайцева, китайская живопись

  Тася, ученица школы № 625, в 8 лет уже освоила технику рисунка по древней китайской технологии…

• Мария Фролова, игра на ксилофоне

  Мария, ученица школы «Феникс», уже в 12 лет в совершенстве освоила технику и нюансы игры. ..

• Варвара, актриса Театра юных москвичей Московского дворца пионеров

  Варвара, ученица школы № 2087 «Открытие», уже исполняет главные роли в спектаклях и снимается…

• София Филина, кружок «Лоскутки» центра художественного образования

  9-летняя София шьет одежду и забавные игрушки, сама придумывает их дизайн. Свой талант она…

• Никита Шилков, судомоделирование

  Чтобы строить масштабные модели кораблей, нужны внимательность, аккуратность, терпение, и,. ..

Проект «Город как школа»

В рамках общегородского проекта «Город как школа» кружки и секции для детей проводятся в технопарках, технополисах, федеральных вузах, музеях, театрах, парках, центрах технологической поддержки образования, на предприятиях и других объектах социальной и научной сфер города.

Школы искусств

Если сфера интересов вашего ребенка — музыка, рисование и другое творчество, то вы можете выбрать занятия на базе школ искусств Департамента культуры.

Спортшколы

Спортивные секции работают в каждом административном округе города Москвы не только на базе образовательных организаций, но и в спортивных школах и других подведомственных учреждениях Москомспорта. У юных москвичей есть возможность попробовать себя в самых разных видах спорта: от хоккея и чирлидинга до плавания и шахмат.

Экология

Поучаствовать в различных кружках и секциях экологической направленности можно в государственном природоохранном бюджетном учреждении «Мосприрода», которое занимается развитием всех московских природных парков и заказников.

Инструкция: как записаться в секцию, кружок или дом творчества

Услуга доступна онлайн на официальном сайте Мэра Москвы — mos.ru.

• зайти в раздел «Услуги»,
• далее выбрать — «Образование»,
• далее — «Дополнительное образование»,
• далее — «Запись в кружки, спортивные секции, дома творчества»,
• далее — «Получить услугу»,
• заполнить необходимые поля.

Чтобы найти нужный кружок на mos.ru, в поиске можно указать ключевые слова, этап обучения (начинающий или продолжающий), район, ближайшую станцию метро, вид деятельности, возраст ребенка, удобное время занятий.

Ребенка до 14 лет в кружки записывают родители (законные представители).

Подростки с 14 лет могут сделать это самостоятельно.

Практически во всех кружках и секциях создана инклюзивная среда, и дети с особыми образовательными потребностями, если нет противопоказаний, могут заниматься наравне со всеми.

Подать заявление можно на дополнительную общеобразовательную программу как на бюджетной, так и платной основе.

МБОУ «Средняя общеобразовательная школа № 57 с углубленным изучением английского языка г. Владивостока». Кружки и секции

Главная
→
Кружки и секции

Кружки и секции на 2022-2023 учебный год

Научно-образовательный центр «Империя школ»
При поддержке «Образование Приморского края»

Юридический адрес МБОУ «СОШ № 57»:

690037, г.Владивосток, ул. Адмирала Юмашева, 12г

Тел.: (423) 244-00-96

Важность конических сечений в математике средней школы – GoGreenva.org

Есть много важных тем, которые можно преподавать на уроках математики в средней школе, но одна из них часто упускается из виду – это конические сечения. Хотя конические сечения могут показаться сложной темой, на самом деле они очень важны для учащихся. Конические сечения — это тип кривой, которая может быть образована, когда плоскость пересекает конус. Существует четыре типа конических сечений: окружности, эллипсы, параболы и гиперболы. Каждый тип конического сечения имеет свои уникальные свойства, которые можно изучать. Круги — самый простой тип конического сечения. Они образуются, когда плоскость пересекает конус в его вершине. Полученная кривая представляет собой идеальный круг. Эллипсы образуются, когда плоскость пересекает конус под углом. Полученная кривая представляет собой эллипс. Параболы образуются, когда плоскость пересекает конус под прямым углом. Полученная кривая представляет собой параболу. Гиперболы создаются, когда плоскость пересекает конус под косым углом. Полученная кривая является гиперболой. Конические сечения важны для изучения учащимися, поскольку они являются частью многих реальных приложений . Например, конические сечения используются в архитектуре, технике и даже астрономии. Изучая конические сечения, студенты могут лучше понять эти приложения в реальном мире.

Почему важно изучать конические сечения?

Источник изображения: pinimg

Конформные сечения используются в различных инженерных приложениях, включая математику, физику и астрономию. В аэродинамике требуется гладкая поверхность для поддержания ламинарного потока и предотвращения турбулентности, а конические сечения должны быть гладкими, чтобы это могло произойти.

Конформные кривые , представляющие собой пересечения поверхностей конусов и плоскостей, являются основой математики. Греческие математики изучали конические сечения более века. В реальной жизни гипербола может использоваться для самых разных целей. В строительстве мостов много гипербол.

R2, где r — радиус окружности, а t(n). Формула эллипса: *(a-b), где a и b — полуоси, и это формула эллипса. Как показано на формула параболы , y — точка пересечения с осью y, а x — точка пересечения с осью x. Гипербола вычисляется как *(a-b)2+c2, которая определяется как полуоси b, c и a.

Коническое сечение Урок

Источник изображения: slidesharecdn

Коническое сечение — это кривая, образованная пересечением плоскости и конуса. Тремя наиболее распространенными типами конических сечений являются круг, эллипс и гипербола.

Коническое сечение — это уникальный тип кривой. Плоскость и двухконусный конус являются наиболее важными примерами этой концепции. На приведенном ниже рисунке показано, как парабола, эллипс, окружность и 9Гипербола 0003 образует гиперболу при пересечении конуса и плоскости. Вы можете узнать больше об этих кривых, нажав на графику. Технологический поток описывает коническое сечение как гиперболу. Чтобы задать первому уровню вопрос: «Одинаковы ли коэффициенты при возведении в квадрат слагаемых?» Изучив коэффициенты, мы должны сделать вывод, что они не совпадают. Поскольку это не парабола, мы должны перейти на второй уровень, как и планировалось.

Ответ (d) является правильным ответом на этот вопрос. Овальные сечения считаются коническими сечениями, потому что в овале нет точек пересечения с плоскостью. Результат пересечения двух плоскостей с осью конуса – круг.

Как ввести коническое сечение?

Существует пересечение между плоскостью и двойным прямым круговым конусом , известное как коническое сечение. В отличие от конуса, наклон пересекающейся плоскости должен быть больше. Общее уравнение для любого конического сечения одинаково. Ax2+Bxy=Ey+F=0, где A, B, C, D, E и F — константы C, D, E и F.

Конические сечения — простая глава?

Если вы будете следовать этим решенным вопросам во время экзаменов, вы сможете развеять любые сомнения, которые могут у вас возникнуть. Решения в этом разделе помогут вам понять разделы 11 как с критической, так и с логической точки зрения. Парабола — одна из самых известных коник.

Значение конических сечений в искусстве

Конические сечения играют важную роль в искусстве, особенно в архитектуре и скульптуре. Они используются для создания ощущения движения и потока в дизайне и могут использоваться для создания как органических, так и геометрических форм . В архитектуре конические сечения часто используются для создания арок и других изогнутых форм, а в скульптуре их можно использовать для создания ощущения движения и потока в дизайне.

Изогнутая линия проходит от точки (x,y) до точки (x,dx,y). Парабола имеет уравнение Y=ax2. Максимальная и минимальная точки кривой могут быть описаны с использованием только одной точки (x, y). Коника это плоская кривая , которая может быть получена путем пересечения конуса с плоскостью.

Конические сечения Human Conics Учебное пособие

Коническое сечение представляет собой кривую, полученную пересечением конуса и плоскости. Существует четыре типа конических сечений: окружность, эллипс, гипербола и парабола. Каждый тип конического сечения имеет свои особые свойства и уравнения.
Круг – это коническое сечение с наибольшей площадью. Он получается, когда плоскость пересекает конус перпендикулярно его оси симметрии. Уравнение окружности: x2 + y2 = r2, где r — радиус окружности.
Эллипс – это коническое сечение со второй по величине площадью. Он получается, когда плоскость пересекает конус под углом, не перпендикулярным его оси симметрии. Уравнение эллипса: x2/a2 + y2/b2 = 1, где a и b — большая и малая полуоси эллипса соответственно.
Гипербола — это коническое сечение с третьей по величине площадью. Он получается, когда плоскость пересекает конус под углом, перпендикулярным его оси симметрии. Уравнение гиперболы имеет вид x2/a2 – y2/b2 = 1, где a и b — большая и малая полуоси гиперболы соответственно.
Парабола – это коническое сечение с четвертой по величине площадью. Уравнение параболы: y2 = 4px, где p — фокус параболы.

В зависимости от плоскости и положения конуса возможны три варианта. Аполлонию (ок. 262–190 до н. э.) приписывают введение термина «коническое сечение» первым, кто это сделал. Классическая тема в истории математики, консекции, вдохновила множество нововведений на протяжении веков. Среди известных авторов конических сечений были Ньютон, Данделин, Жергонн, Понселе, Брианшон, Дюпен, Шасль и Штайнер. Более поздние математики внесли большой вклад в развитие проективной геометрии. Учащиеся, занимающиеся драматическим искусством, имеют возможность выражать свои эмоции, мысли и мечты в безопасной и контролируемой среде.

Связи в классе — Коники

Common Core написан для того, чтобы учащиеся изучали коники с двух точек зрения: геометрических описаний (графических представлений) и уравнений. Если учащиеся охватывают только необходимый материал, учителя не дадут своим ученикам возможности изучить больше, чем необходимый минимум. Даже когда некоторые преподаватели включают происхождение конических сечений как производное от пересечения плоскости и конуса, мало что делается для развития связей между трехмерными представлениями, графиками на декартовой плоскости и их уравнениями.

Общие базовые стандарты, связанные с кониками, появляются в математике средней школы как:

Выражение геометрических свойств с помощью уравнений (G.GPE)
Перевод между геометрическим описанием и уравнением для конического сечения
1. Выведите уравнение окружности с заданным центром и радиусом по теореме Пифагора; заполните квадрат, чтобы найти центр и радиус круга, заданного уравнением.
2. Выведите уравнение параболы с учетом фокуса и директрисы.
3. (+) Вывести уравнения эллипсов и гипербол для заданных фокусов, используя тот факт, что сумма или разность расстояний от фокусов постоянны.

Несмотря на то, что он не фигурирует в том же наборе стандартов, раздел «Геометрические измерения и размеры» можно использовать на вводных уроках по коническим сечениям.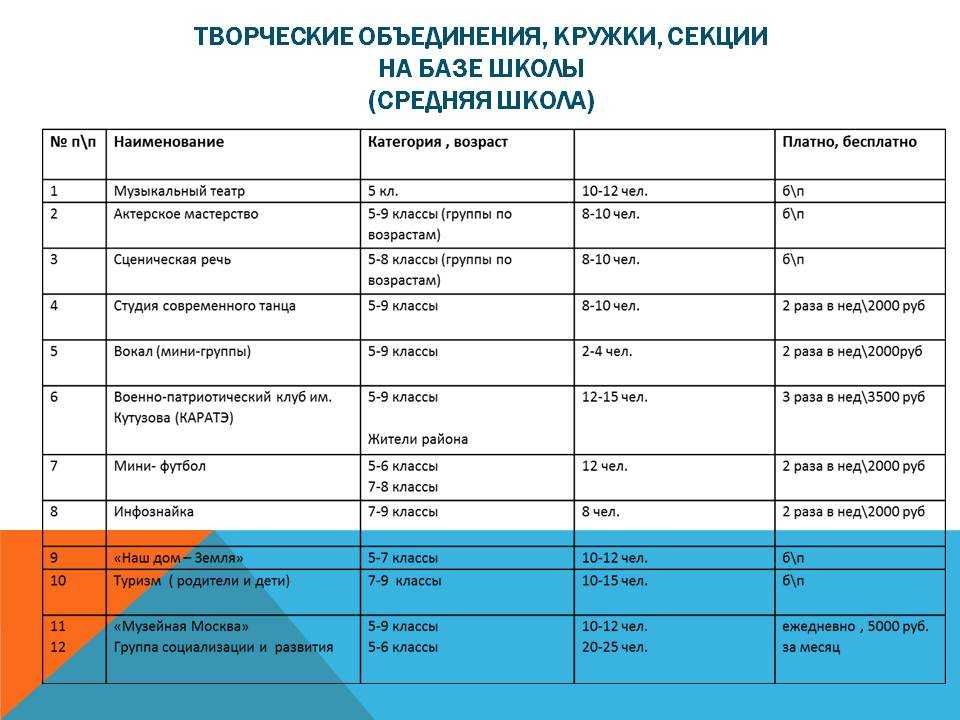 Этот стандарт выглядит следующим образом:

Геометрические измерения и размеры (G.GMD)
Визуализация отношений между двухмерными и трехмерными объектами
Определение формы двумерных поперечных сечений трехмерных объектов и определение трехмерных объектов, созданных вращением двухмерных объектов.

Для более подробного ознакомления с коническими сечениями инструкторы могут начать с изучения двумерных поперечных сечений трехмерных фигур. Это понятие впервые появляется в программе средней школы; поэтому учителя должны быть уверены, что учащиеся уже освоили его. После повторного ознакомления с двухмерными сечениями более простых трехмерных фигур (например, кубов, призм, цилиндров и пирамид) класс может сосредоточить свое внимание на конусах (в конечном итоге на конусах с двойным ворсом).

Пересечение плоскости с конусом с двойным швом может быть представлено с помощью функции графического калькулятора на компьютере, изображений и анимации с помощью веб-поиска, физических манипуляций и фонарика.

Учителя также могут захотеть предоставить базовую историю конических открытий древнегреческими математиками, такими как Менехм, Евклид, Аристей, Архимед и, конечно же, Аполлоний. Оттуда инструкторы могут связать астрономию, обсуждая открытие Кеплером эллиптических орбит планет. Эта историческая перспектива может быть использована в качестве крючка для привлечения интереса учащихся.

Стандарты требуют, чтобы учащиеся умели выводить уравнения окружностей, парабол, эллипсов и гипербол с учетом конкретных рекомендаций. Важно, чтобы учащиеся также могли вывести уравнение каждого конического сечения с помощью других средств, а не только того, что дано в стандартах Common Core, чтобы установить связи и улучшить концептуальное понимание.

Преподаватели должны обеспечить, чтобы учащиеся могли изобразить каждую фигуру в виде графика, пометить соответствующие части этого графика и установить связи между уравнениями и графиками. При наличии апплетов и других технологий учащимся будет напрасно рисовать каждую коническую секцию только с помощью бумаги и карандаша. Desmos, графические калькуляторы и блокнот Geometer’s Sketchpad — все это захватывающие средства для исследования того, как строить, манипулировать и исследовать коники способами, которые были недоступны десятилетия назад.

В классе стандарты следует рассматривать как уровень знаний. Это означает, что инструкторы должны учить своих студентов не меньшему, чем указано в стандартах, но всегда должны стараться предоставить больше инструментов и более глубокие знания. Чем шире разнообразие материала, с которым сталкивается учащийся, тем больше у него шансов осознать свою истинную страсть.

Для получения дополнительных ресурсов и потенциальных идей для уроков, пожалуйста, посетите:
        Conic Flyer
Коническая секция Explorer
Секция конической секции Урок Урок Планы и научного центра
Резка коники
фонарики и конические секции
Человеческие Conics
Учебный блок: CONIC SECES

СПИСАМИ
СРЕДНЯЯ ШКОЛА: Геометрия ».