что носить, какая одежда подойдет

Изящными изгибами и аппетитными формами фигура, похожая на прямоугольник, не отличается. Зато такая внешность считается модельной. Правильная одежда способна замаскировать ее главный недостаток – отсутствие талии. Осталось подобрать гардероб. Легко ли девушкам сделать это с такими параметрами? Разбираем стройную и полную версию прямоугольной фигуры при помощи автора «Модного блога» Анастасии Алексеенко.

Теги:

Анастасия Алексеенко

Мода

Модные тренды

Лайфхаки

Модные блоги

Getty Images

Анастасия Алексеенко

Автор «Модного блога»

Для начала обозначим, какую фигуру называют прямоугольником. Это когда у девушки плечи, талия и бедра по ширине примерно одинаковые. Представительницы прекрасного пола с подобными формами могут похвастаться пропорциональностью верхней и нижней частей тела, аккуратными ягодицами, тонкими руками и стройными ногами.

Стоит девушке с типом фигуры «прямоугольник» набрать лишний вес, как усугубляется проблема из разряда «что носить». Обладательницы такого тела итак иногда недовольны своим неженственным, мальчишеским видом. А так называемый спасательный круг из жировых запасов прибавляет торсу грузности и плотности. При любом раскладе это твоя внешность и для нее всегда можно подобрать большой выбор фасонов. И мы подскажем, какие самые выигрышные.

Что собой представляет тип фигуры «прямоугольник»

Итак, существуют разные комплекции женщин, которые чаще всего делят на пять основных типов. Среди них груша, прямоугольник, песочные часы, треугольник и яблоко.

В рассматриваемой нами фигуре «прямоугольник» выделяются стройный и полный варианты, показанные на картинке ниже.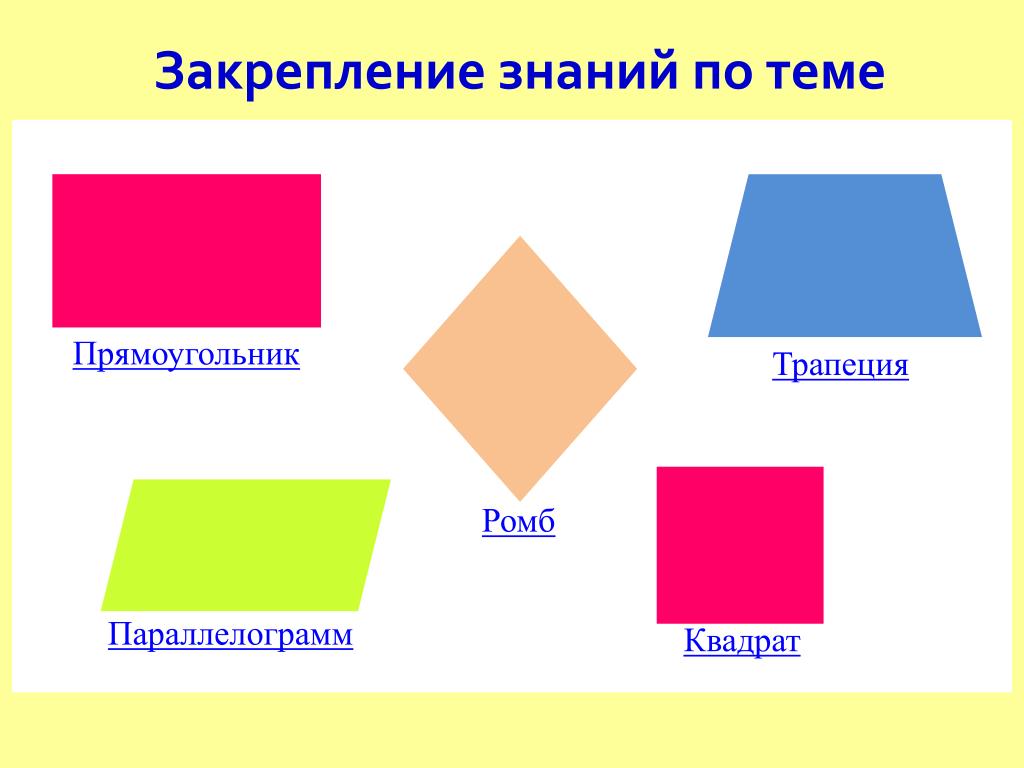 Их иногда еще называют I-тип и H-тип, «стройная колонна» и «полная колонна». Как определить, что у тебя фигура «прямоугольник»? Просто замерить обхват груди, бедер и талии и сравнить значения.

РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ

Если разница между талией и бедрами менее 22 см, то ты обладательница данного типа телосложения. Рассмотрим, что собой представляют разновидности фигуры «прямоугольник» и выделим их признаки.

Стройная колонна

Одежда для типа фигуры «стройный прямоугольник» подбирается очень легко. По факту речь идет о комплекции большинства моделей. С помощью гардероба для стандартных параметров можно выстроить практически любой силуэт. Наверное, потому он и царит на подиуме, что позволяет дизайнерам реализовывать свои идеи. Талия у такого типа обычно не очень выражена, и «посадить» вещь удобнее и легче, чем при изгибистых формах.

Среди голливудских и российских актрис и спортсменок выделяются знаменитости, у которых ярко выраженная фигура «прямоугольник». Стройный тип у Кэмерон Диас, Киры Найтли, Джессики Альбы, Милы Йовович, Анны Курниковой, Натали Портман. У этих звезд нет выдающейся груди, они худые и создают видимость талии с помощью удачно подобранных луков.

Многие модели с фигурой «прямоугольник» добились серьезных успехов на подиуме. Именно их для своих показов выбирают именитые модельеры. Всему миру известны имена Натальи Водяновой, Жизель Бюндхен, Миши Бартон, Кейт Мосс.

Полная колонна

Здесь женщина уже меньше напоминает модель из-за несколько расплывшейся талии и, как правило, более выраженной груди. Чем больше лишних кило, тем менее спортивным и атлетическим выглядит телосложение. Часто жир откладывается в верхней части живота, может распределиться и на бедрах.

Среди знаменитостей примеры полноватой колонны демонстрируют Бритни Спирс, Лайза Минелли, Тина Тернер. В разные периоды жизни эти женщины худели и поправлялись, и «прямоугольник» становился еще выразительнее.

Хотя такой тип отдельно не выделяют, данная фигура больше напоминает перевернутый прямоугольник – его широкие стороны стремятся сменить вертикаль на горизонт. Зато ноги остаются стройными, не считая образовавшихся запасов на бедрах. Поэтому нужно не бояться подчеркивать достоинства, в том числе и бюст, которым наградила природа.

Рекомендуем модельному типу фигуры не «расползаться», питаться правильно и следить за весом. Это не только вредит здоровью. Гардероб также подбирать значительно сложнее.

Одежда для фигуры «прямоугольник»: что можно и нельзя носить

Раз комплекция немного схожа с мужской, твоя задача сделать ее более женственной. Нужно постараться смягчить угловатые плечи и резкие линии. В нашей подборке фото ты можешь увидеть женщин с фигурой «прямоугольник», которые отдали предпочтение фасонам, повторяющим силуэт. Одежда не должна слишком прилегать, пусть будет немного свободной.

Мы расскажем основные моменты, на которые следует обратить внимание, учитывая параметры фигуры «прямоугольник».

Табу для фигуры «прямоугольник»: примеры неудачных образов

Казалось бы, фигура у девушки «прямоугольник», значит, она модельная, носи, что хочешь. Но есть варианты одежды, которые значительно ухудшают пропорции и портят общий вид. Вот несколько примеров:

• большой объем одного цвета и фактуры без разделения на зоны (в случае, например, с платьем из однотонного кружева тоненький поясок существенно улучшил бы ситуацию)
• «прямоугольникам» могут не подходить платья с резинкой на талии. Зависит, конечно, от каждого конкретного платья — ткани, густоты сборки и так далее, но часто такие платья делают девушку на вид крупнее, чем она есть на самом деле
• ну и, конечно, необходимо аккуратно относиться к крою, который вытягивает торс, подчеркивая его «прямоугольность»

Впрочем, лично мне последнее утверждение не кажется абсолютным правилом. Хотя в целом считается, что мы должны выстраивать правильные пропорции, близкие к стройным песочным часам, но фигура типа «прямоугольник» очень популярна и многим такое тело нравится.

Большое количество женщин других типов могут стремиться именно к ней. А значит, что сама девушка с подобной фигурой может считать, что подчеркивать «прямоугольность» — это своего рода фишка. В общем, я советую в этом вопросе отталкиваться от собственных эстетических предпочтений.

Оптические иллюзии для типа фигуры «прямоугольник»: примеры фото

Если же ты все-таки хочешь побрать для фигуры «прямоугольник» более женственные платья, создать плавные линии, варианты есть. Примеряй модели с драпировки в нужных местах.

• Подчеркнуть линию талии поможет отрезной крой или оптические иллюзии, основанные на контрастных цветах.

• Но будь аккуратна: подчеркивая линию талии, ты не должна делать эту зону излишне широкой. Иначе получим эффект прямо противоположный желаемому.

Какая одежда подходит «прямоугольнику»

Стройным девушкам с такими формами практически всегда идут многослойные комплекты.

В случае с фигурой у человека Н-типа («полная колонна» или «полный прямоугольник») работают практические все правила, что и для стройных. Единственное, чему стоит уделить больше внимания — линия талии. Иногда девушки такого типа склонны набирать лишний вес как раз в этой зоне.

Какие платья следует подобрать под фигуру «прямоугольник»? Спасением будут и прямые силуэты и многослойные комплекты. Отвлекаем внимание от лишнего, акцентируя его на самых выигрышных частях тела! Линию талии можно удачно маскировать блузами и топами навыпуск, если в этой зоне находятся отложения. А приталенный жакет создаст видимость талии.

Анастасия Алексеенко, автор Модного блога

Инструменты выделения фигур — Служба поддержки Майкрософт

Visio, план 2 Visio профессиональный 2021 Visio стандартный 2021 Visio профессиональный 2019 Visio стандартный 2019 Visio профессиональный 2016 Visio стандартный 2016 Visio профессиональный 2013 Visio 2013 Еще. ..Меньше

Как правило, чтобы внести изменения в фигуру, ее сначала нужно выделить, а для некоторых изменений нужно выделять сразу несколько фигур. В этой статье описано несколько способов выделения фигур в разделе Быстрые задачи.

Примечание: Если фигуру в документе не удается выделить, переместить, увеличить, уменьшить или повернуть, возможно, она является частью заблокированного слоя.

Разблокирование слоя

1. На вкладке Главная в группе Редактирование нажмите кнопку Слои и выберите команду Свойства слоя.

2. В окне Свойства слоя в столбце Блокировка снимите флажок, связанный с типом фигуры, которую нужно выделить.

Что такое прямоугольник? Определение, примеры, формулы, факты

Что такое прямоугольник?

Прямоугольник — это замкнутая двумерная фигура, имеющая 4 стороны, 4 угла и 4 прямых угла (90°). Противоположные стороны прямоугольника равны и параллельны. Поскольку прямоугольник представляет собой двумерную форму, он характеризуется двумя измерениями: длиной и шириной. Длина – это длинная сторона прямоугольника, а ширина – меньшая сторона.

Родственные игры

Прямоугольники вокруг нас

Прямоугольник — самая распространенная фигура, которая является частью нашей повседневной жизни. Некоторые реальные примеры прямоугольника приведены ниже.

Связанные рабочие листы

Что еще мы можем назвать прямоугольником?

• Поскольку все углы прямоугольника равны, мы также называем его равноугольным четырехугольником . Четырехугольник – это четырехсторонняя замкнутая фигура.
• Поскольку стороны прямоугольника параллельны, мы также можем назвать его прямоугольным параллелограммом . Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны. Прямоугольники являются частным случаем параллеграммов.

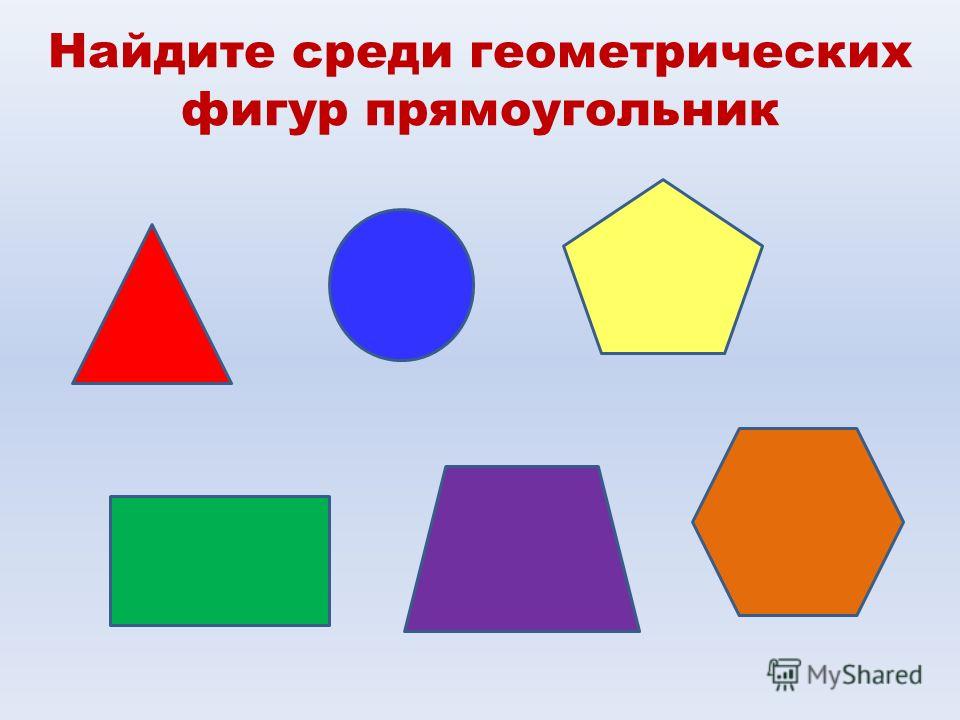
Что такое диагональ прямоугольника?

Отрезки, соединяющие противоположные углы прямоугольника, называются диагоналями. На данном рисунке две диагонали прямоугольника AC и BD. Диагонали прямоугольника имеют одинаковую длину. Следовательно, АС = BD.

Если мы знаем длину и ширину прямоугольника, мы можем использовать теорему Пифагора, чтобы найти длину его диагонали.

На данном рисунке ADB образует треугольник с прямым углом в точке A. Диагональ (BD) прямоугольника образует его гипотенузу. 9{2}}$

Свойства прямоугольника

Ниже приведены свойства прямоугольника:

1. Это плоская замкнутая форма.
2. Имеет 4 стороны, 4 угла и 4 угла (вершины).
3. Имеет 2 размера, а именно длину и ширину
4. Каждый угол прямоугольника равен 90°.
5. Противоположные стороны равны и параллельны.
6. Имеет 2 диагонали одинаковой длины.

Площадь и периметр прямоугольника

Площадь прямоугольника

Пространство, занимаемое прямоугольником, называется его площадью. Площадь прямоугольника можно вычислить, найдя произведение его длины на ширину. Итак,

Площадь прямоугольника = длина × ширина

Поскольку площадь прямоугольника является произведением длины и ширины, она измеряется в квадратных единицах, например, в квадратных метрах (м ² ), кв. дюймов (в ² ) и так далее.

Периметр прямоугольника

Периметр прямоугольника равен сумме длин его четырех сторон. Найдем формулу периметра прямоугольника.

Периметр прямоугольника = длина + ширина + длина + ширина

= 2 × длина + 2 × ширина

= 2 (длина + ширина)

Поскольку мы добавляем единицы длины, чтобы найти периметр, его единицей также является 

Периметр измеряется в единицах длины (дюймы, футы, метры и т. д.), потому что мы складываем длины сторон, чтобы найти ответ.

Интересные факты

1. Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками
2. Диагонали прямоугольника делят прямоугольник на четыре треугольника
3. Каждый квадрат является прямоугольником, но каждый прямоугольник не является квадратом

Решенные примеры

1. Определите прямоугольники на данных рисунках.

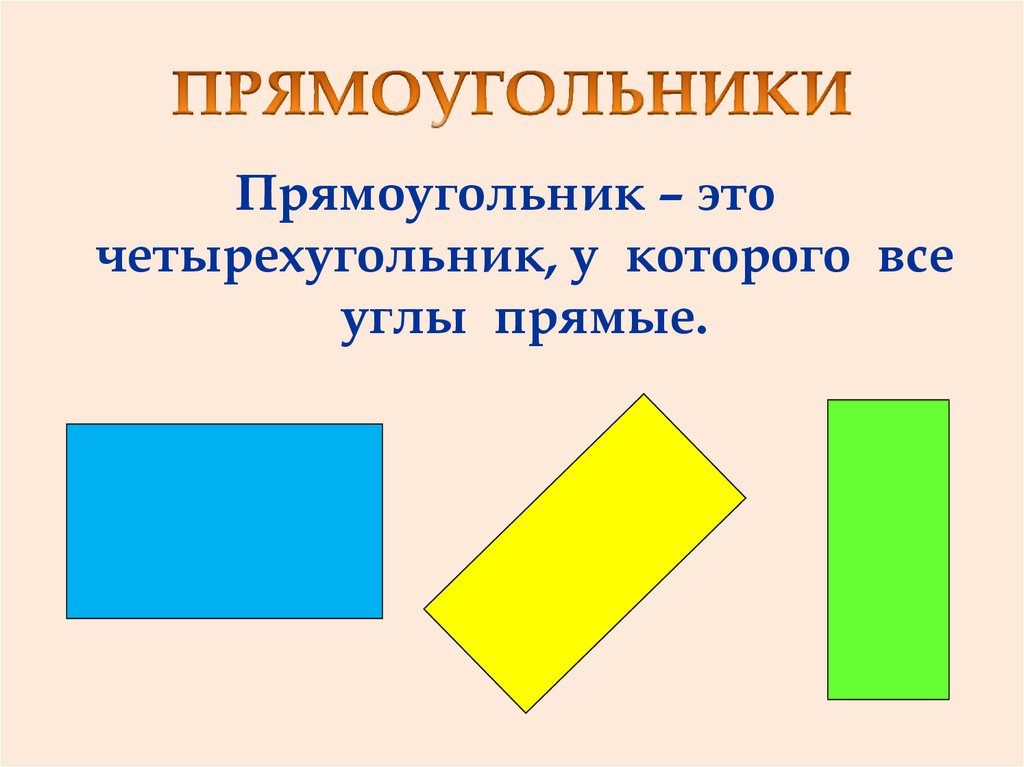
Решение: 

Фигуры A и D являются прямоугольниками, поскольку у них противоположные стороны равны и параллельны, а все четыре угла прямые.

2. Определите длину, ширину и диагональ данного прямоугольника.

Решение:

Длина → PQ и RS

Ширина → SP и RQ

Диагонали → PR и QS

3. Длина и ширина прямоугольника равны 7 дюймам и 21 дюйму соответственно. Найдите его периметр.

Решение:

Периметр прямоугольника = 2 × (длина + ширина)

                                                                                     = 2 × (7 + 21) дюймов

= 2 × (28) дюймов

= 56 дюймов

4. Длина и ширина прямоугольника составляют 0,3 м и 15 см. Найдите его площадь.

Решение:

Длина = 0,3 м и Ширина = 15 см

Длина и ширина прямоугольника различны, поэтому преобразуем одно из них.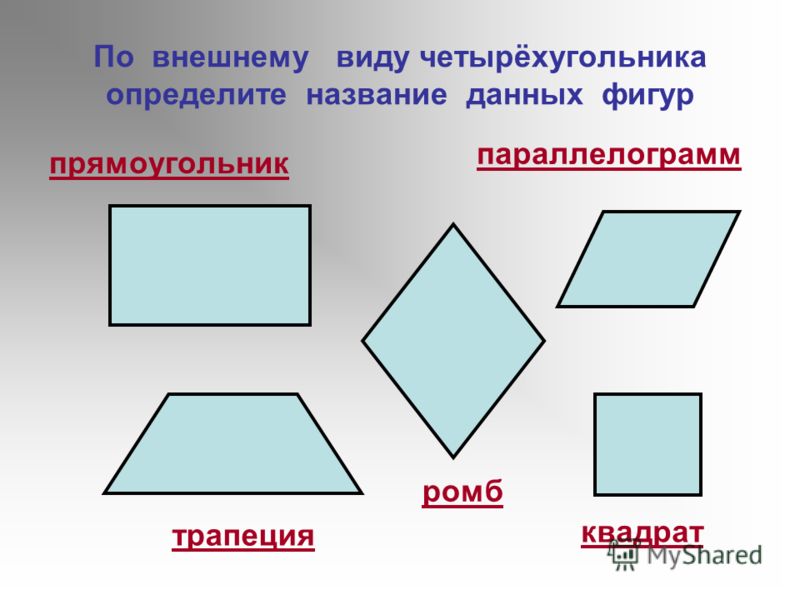 Переведем длину в сантиметры, умножив ее на 100, потому что 1 м = 100 см. 9{2}} = \sqrt{64+36} = \sqrt{100} = \sqrt{10 ✕ 10}$ = 10 дюймов

Практические задачи

1

Какова площадь прямоугольного картона длиной 1 м и шириной 30 см?

30 кв. см

300 кв. см

3 000 кв. см

30 000 кв. см

Правильный ответ: 3 000 кв. см
Длина картона = 1 м = 100 см и ширина
Площадь прямоугольного картона = 100 см ✕ 30 см = 3000 кв. см

2

Каков периметр прямоугольника длиной 16 футов и шириной 7 футов?

23 фута

46 футов

112 футов

305 футов

Правильный ответ: 46 футов
Периметр = 2 × (16 + 7) см = 2 × 23 фута = 06 9000

3 Что такое ширина прямоугольника, длина и площадь которого равны 8 см и 32 см2 соответственно?

256 см

4 см

40 см

80 см

Правильный ответ: 4 см

Часто задаваемые вопросы

Что такое прямоугольник?

Прямоугольник — это замкнутая двумерная фигура, имеющая 4 стороны, 4 угла и 4 прямых угла (90°). Противоположные стороны прямоугольника равны и параллельны.

Какие есть реальные примеры прямоугольников?

Некоторые реальные примеры прямоугольника включают книги, дверь, столешницу, доску и т. д.

В чем разница между прямоугольником и параллелограммом.

Все стороны квадрата равны, тогда как противоположные стороны прямоугольника равны и параллельны.

Почему все прямоугольники не квадраты?

Все прямоугольники не являются квадратами, потому что по определению прямоугольника его противоположные стороны должны быть равны, но его соседние стороны могут быть или могут быть равными. Таким образом, только прямоугольники с равными смежными сторонами являются квадратами.

Прямоугольник — Формулы | Определение | Примеры

Прямоугольник представляет собой четырехугольник, в котором все углы равны, а противоположные стороны равны и параллельны. Вокруг нас много прямоугольных объектов.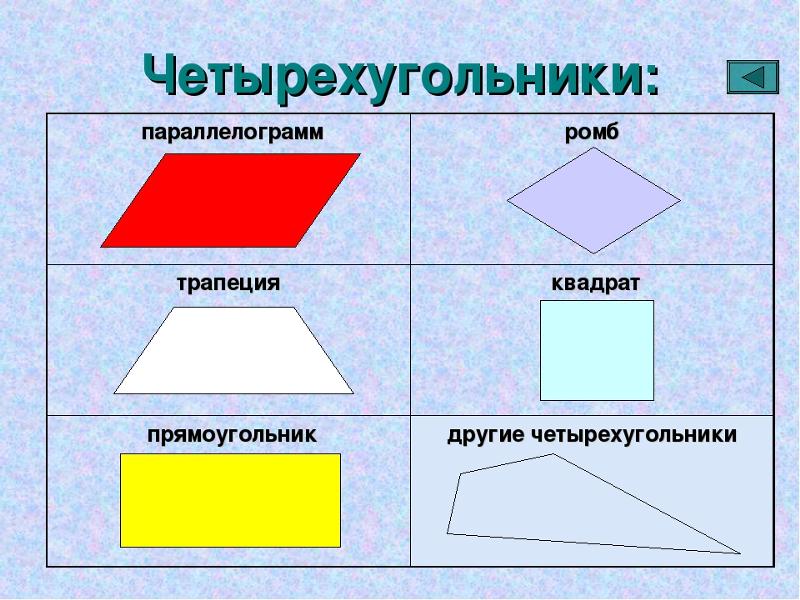 Каждая прямоугольная форма характеризуется двумя размерами, его длиной и шириной. Более длинная сторона прямоугольника известна как длина, а более короткая сторона известна как ширина. В этой главе мы узнаем о форме прямоугольника, некоторых формулах прямоугольника, типах прямоугольников и их свойствах.

1.	Что такое прямоугольник?
2.	Свойства прямоугольника
3.	Диагональ прямоугольника
4.	Площадь прямоугольника
5.	Периметр прямоугольника
6.	Часто задаваемые вопросы о прямоугольнике

Что такое прямоугольник?

Прямоугольник представляет собой замкнутую двумерную фигуру с четырьмя сторонами. Противоположные стороны прямоугольника равны и параллельны друг другу, а все углы прямоугольника равны 90°.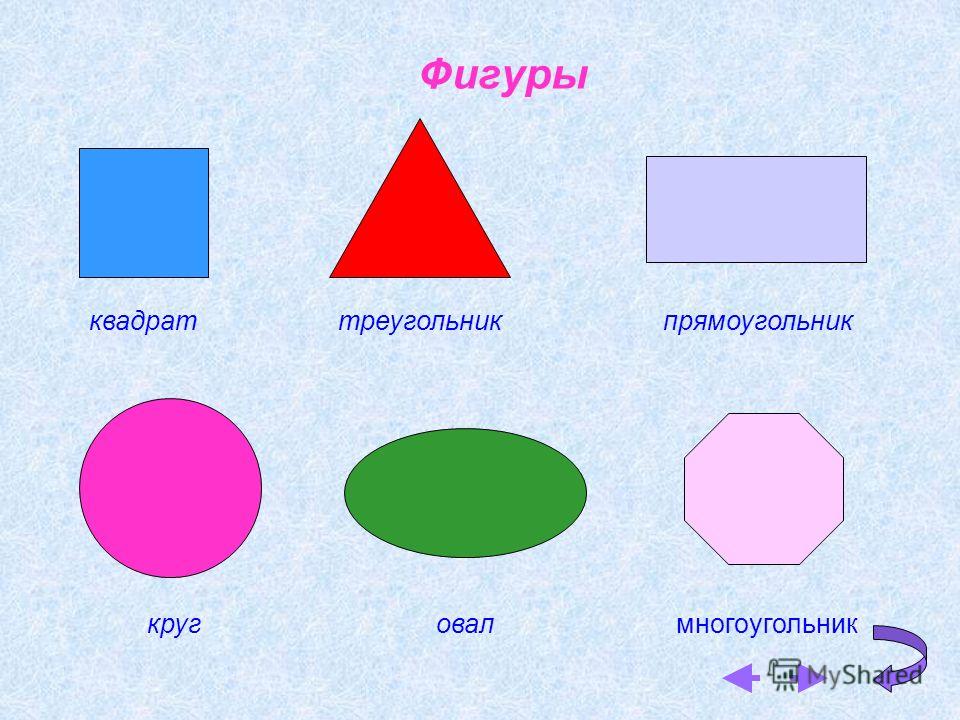 Посмотрите на прямоугольник, приведенный ниже, чтобы увидеть его форму, стороны и углы.

Определение прямоугольника

Определение прямоугольника гласит, что прямоугольник представляет собой двумерную фигуру с 4 сторонами, 4 вершинами и 4 внутренними прямыми углами. Противоположные стороны прямоугольника равны и параллельны.

Длина и ширина прямоугольника

Длина прямоугольника относится к большей стороне, а ширина прямоугольника относится к меньшей стороне. Следует отметить, что длину прямоугольника можно вычислить, если известны площадь, периметр и ширина прямоугольника. Точно так же можно рассчитать ширину прямоугольника, если известны площадь, периметр и длина прямоугольника.

Свойства прямоугольника

Прямоугольник – это замкнутая фигура, имеющая четыре стороны и угол между соседними сторонами, равный 90°. Прямоугольник может иметь широкий спектр свойств. Некоторые из важных свойств прямоугольника приведены ниже.

• Прямоугольник — это четырехугольник.
• Противоположные стороны прямоугольника равны и параллельны друг другу.
• Внутренний угол прямоугольника при каждой вершине равен 90°.
• Сумма всех внутренних углов равна 360°.
• Диагонали делят друг друга пополам.
• Длины диагоналей равны.
• Длину диагоналей можно получить с помощью теоремы Пифагора. Длина диагонали со сторонами a и b равна, диагональ = √( a ² + b ² ).
• Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
• Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.

Формулы прямоугольника

У прямоугольника есть несколько основных формул, которые можно запомнить, чтобы найти отсутствующие или неизвестные значения. Несколько формул прямоугольника приведены ниже:

• Формула площади прямоугольника: Если мы знаем длину и ширину прямоугольника, мы можем найти площадь, используя формулу Площадь прямоугольника = Длина × Ширина
• Формула периметра прямоугольника: Если мы знаем длину и ширину прямоугольника, мы можем найти периметр, используя формулу Периметр прямоугольника = 2 (длина + ширина)
• Формула длины прямоугольника: Если мы знаем площадь и ширину прямоугольника, мы можем найти длину , используя формулу площади путем подстановки значений, или мы можем переформулировать формулу площади следующим образом: Длина = Площадь прямоугольника ÷ Ширина. Точно так же, если мы знаем периметр и ширину прямоугольника, мы можем найти длину , используя формулу периметра, подставив значения, или мы можем переформулировать формулу периметра как Длина = (Периметр ÷ 2) — Ширина
• Формула ширины прямоугольника: Если мы знаем площадь и длину прямоугольника, мы можем найти ширину , используя формулу площади, подставив значения, или мы можем переформулировать формулу площади следующим образом: Ширина = Площадь прямоугольника ÷ Длина. Точно так же, если мы знаем периметр и длину прямоугольника, мы можем найти ширину , используя формулу периметра, подставив значения, или мы можем перефразировать формулу периметра как, Ширина = (Периметр ÷ 2) — Длина

Диагональ прямоугольника

Диагональ прямоугольника — это отрезок, соединяющий любые две его несмежные вершины. В следующем прямоугольнике AC и BD — диагонали, имеющие одинаковую длину. Диагональ делит прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.

Диагональ прямоугольника Формула

Формула диагонали прямоугольника выводится с помощью теоремы Пифагора. Следуя приведенному выше рисунку, рассмотрим прямоугольник длины l и ширины w. Пусть длина каждой диагонали равна d. Применяя теорему Пифагора к треугольнику ABD, d ² = l ² + w ² . Извлекая квадратный корень с обеих сторон, √(d ² ) = √(l ² + w ² ). Таким образом, формула диагонали прямоугольника равна диагонали (d): √(l² + w²) и, таким образом, диагонали прямоугольника можно вычислить, когда длина и ширина прямоугольника известны.

Диагональ прямоугольника (d) = √(l² + w²)

Площадь прямоугольника

Площадь прямоугольника — это количество единичных квадратов, которые могут поместиться в прямоугольник. Другими словами, пространство, занимаемое прямоугольником, является площадью прямоугольника. Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов ноутбуков, классных досок, холста для рисования и т. Д. Мы можем использовать формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами. Например, давайте рассмотрим прямоугольник длиной 4 дюйма и шириной 3 дюйма. Нарисуем единичные квадраты внутри прямоугольника. Каждый единичный квадрат представляет собой квадрат длиной 1 дюйм. Теперь подсчитайте количество единичных квадратов на рисунке ниже. Сколько квадратов вы можете наблюдать? Всего 12 квадратов. Мы уже знаем, что площадь измеряется в квадратных единицах. Поскольку единица измерения этого прямоугольника дана в дюймах, площадь измеряется и записывается в квадратных дюймах. Таким образом, площадь прямоугольника = 12 квадратных дюймов. Таким образом, площадь прямоугольника можно вычислить, зная его стороны (длину и ширину).

Формула площади прямоугольника

Формула площади прямоугольника , длина и ширина (ширина) которого равны «l» и «w» соответственно, является произведением его длины и ширины, то есть:

Площадь прямоугольника = (д × ш)

Периметр прямоугольника

Периметр прямоугольника — это длина всей границы прямоугольника. Его можно принять как сумму общей меры длины и ширины прямоугольника, и он выражается в линейных единицах, таких как сантиметры, дюймы и так далее. Например, если вам нужно украсить рамку вашего прямоугольного блокнота, вы можете легко рассчитать, сколько ленты вам понадобится, найдя периметр, или если вам нужно поставить забор вокруг вашего сада, периметр сада даст вам точную длину провода, который вам понадобится. Формула, используемая для вычисления периметра прямоугольника, объясняется ниже.

Формула периметра прямоугольника

Формула для периметра ‘P’ прямоугольника, длина и (ширина) ширина которого равны ‘l’ и ‘w’ соответственно, равна 2(l + w).

Формула периметра прямоугольника = 2 (длина + ширина)

Типы прямоугольников

Четырехугольник, у которого противоположные стороны равны, а смежные стороны пересекаются под углом 90°, называется прямоугольником. У прямоугольника две равные диагонали. Длина диагоналей рассчитывается с использованием длины и ширины. Есть два типа прямоугольников:

• Квадрат
• Золотой прямоугольник

Квадрат

Квадрат представляет собой замкнутую двумерную фигуру с четырьмя равными сторонами и четырьмя равными углами. Это тип прямоугольника, у которого все четыре стороны равны. Внутренний угол в каждой вершине равен 90º, что соответствует определению прямоугольника. Обратите внимание на приведенный ниже квадрат, который соответствует всем свойствам прямоугольника.

Золотой прямоугольник

Золотой прямоугольник — это прямоугольник, отношение длины к ширине которого аналогично золотому сечению, 1: (1+⎷5)/2. Его стороны определены по золотому сечению, то есть 1:1,618. Например, если ширина составляет около 1 фута, тогда длина будет равна 1,168 фута.

☛ Похожие статьи

• Свойства прямоугольника
• Разница между квадратом и прямоугольником
• Является ли квадрат прямоугольником?

Часто задаваемые вопросы о прямоугольнике

Что такое прямоугольник в геометрии?

Прямоугольник представляет собой двумерную фигуру (2D-форму), в которой противоположные стороны параллельны и равны друг другу, а все четыре угла прямые. Меньшая сторона прямоугольника называется его шириной (шириной), а длинная сторона – длиной. Одной из самых распространенных геометрических фигур, с которыми мы сталкиваемся в повседневной жизни, является прямоугольник.

☛ Читайте также

• 3D-фигуры
• Геометрические фигуры

Как найти длину прямоугольника?

• Длину прямоугольника можно вычислить, если известны периметр и ширина. Например, если периметр прямоугольника равен 32 единицам, а его ширина равна 4 единицам, мы можем использовать формулу периметра, чтобы получить длину. Периметр прямоугольника = 2 (l + w). Подставим известные значения в формулу, 32 = 2 (длина + 4). Решив это, мы получим длину + 4 = 16, то есть длину = 12 единиц. Точно так же, если площадь прямоугольника и ширина известны, длину можно рассчитать, используя формулу площади прямоугольника и подставив известные значения.
• Другой способ найти длину прямоугольника — использовать следующие формулы, полученные из формул площади и периметра: длина = площадь прямоугольника ÷ ширина; и Длина = (Периметр ÷ 2) — ширина

Как найти ширину прямоугольника?

• Ширину прямоугольника можно вычислить, если известны его площадь и длина. Например, если площадь прямоугольника составляет 48 единиц, а его длина — 12 единиц, мы можем использовать формулу площади, чтобы получить ширину. Площадь прямоугольника = l × w. Подставим известные значения в формулу, 48 = 12 × ширина. Решив это, мы получим ширину = 48/12, то есть ширину = 4 единицы. Точно так же, если периметр прямоугольника и длина известны, ширину можно рассчитать, используя формулу для периметра прямоугольника и подставив известные значения.
• Другой способ найти ширину прямоугольника — использовать следующие формулы, полученные из формул площади и периметра: Ширина = Площадь прямоугольника ÷ Длина; и Ширина = (Периметр ÷ 2) — Длина

Как найти диагональ прямоугольника?

Длину диагонали прямоугольника можно вычислить, если известны длина и ширина. Поскольку диагональ прямоугольника образует со своими сторонами прямоугольный треугольник, диагональ становится гипотенузой, и ее значение можно вычислить с помощью теоремы Пифагора. Например, если длина прямоугольника равна 4 единицам, а ширина равна 3 единицам, мы можем найти длину диагонали, используя формулу, диагональ (d) = √ (л² + ш²). Итак, подставим в него значение длины и ширины. Диагональ (d) = √ (l² + w²) = √ (4² + 3²) = √ (16 + 9) = √ 25 = 5 единиц.

Почему прямоугольник не является правильным многоугольником?

Правильный многоугольник — это многоугольник, у которого все стороны имеют одинаковую длину и все углы имеют одинаковую величину. В прямоугольнике только противоположные стороны имеют одинаковую длину, следовательно, прямоугольник не является правильным многоугольником.

☛ Также проверьте:

• Типы полигонов
• Площадь полигонов

Какая формула площади прямоугольника?

Площадь прямоугольника — это площадь, занимаемая им. Площадь прямоугольника равна произведению его длины на ширину (ширину). Формула вычисления площади прямоугольника: Площадь = L × B; где (L) — длина, а (B) — ширина (ширина) прямоугольника.

☛ Ознакомьтесь со списком формул для простых вычислений:

• Формулы периметра
• Объемные формулы
• Формулы площади поверхности
• Формулы измерения

Каковы свойства прямоугольника?

Основные свойства прямоугольника:

• Противоположные стороны параллельны и равны.
• Все углы равны 90°.
• Диагонали равны и делят друг друга пополам.

Площадь прямоугольника равна площади квадрата?

Нет, площадь квадрата не обязательно равна площади прямоугольника, потому что каждый квадрат является прямоугольником, но не все прямоугольники являются квадратами. Формула для вычисления площади прямоугольника: площадь прямоугольника = длина × ширина, а площадь квадрата = (сторона) ² .

Как найти периметр прямоугольника?

Периметр прямоугольника в два раза больше суммы его длины и ширины и выражается по формуле Периметр = 2 (Длина + Ширина). Он выражается в линейных единицах, таких как см, дюймы и т. д.

Как называется трехмерный прямоугольник?

Трехмерный прямоугольник называется прямоугольной призмой. Прямоугольная призма – это призма, основания которой также являются прямоугольниками. Всего у него 6 граней, из которых 3 пары одинаковых противоположных граней, т. е. в прямоугольной призме все противоположные грани одинаковы.