Достопримечательности Пятигорска: Грот Лермонтова | Дороги мира

Достопримечательностей в Пятигорске очень много. Но так как расположены они довольно компактно, за 2-3 дня можно успеть посмотреть все.

Гулять по таким местам гораздо интереснее, если знаешь их историю. Сегодня предлагаю прогуляться к Гроту Лермонтова.

Находится он на склоне горы Машук, на Михайловском отроге. Небольшую природную пещеру обнаружили братья Бернандацци во время благоустройства Эммануэлевского парка. Они облагородили грот, проложили к нему дорожку, вымощенную камнем. При этом живописность самой пещеры и окружающей её местности была сохранена.

Дорожка к Гроту Лермонтова

Первое упоминание о гроте можно найти в книге главврача Управления вод Фёдора Петровича Конради «Рассуждения о искусственных минеральных водах с приобщений новейших известий о Кавказских минеральных источниках», вышедшей в Санкт-Петербурге в 1831 году. Он писал:

Первоначально пещера очень романтично называлась гротом Калипсо (в переводе имя этой нимфы означает «та, что скрывает»).

Но затем этот грот облюбовал (а впоследствии – прославил) сам Лермонтов. Говорят, он очень любил сидеть здесь, любуясь прекрасными видами вокруг. К тому же отсюда, сверху, было очень удобно наблюдать за «водяным обществом», прогуливающимся у Елизаветинской галереи.

Вид на окрестности от Грота Лермонтова

И действительно, с этого места и в наши дни открывается отличный вид на Елизаветинскую (Академическую) галерею.

Вид на Академическую галерею сверху

После смерти Лермонтова почитатели его таланта приносили к гроту цветы, устраивали тут чтение лермонтовских стихов.

С 1860-х годов грот получил название Лермонтовского, да так и называется до сих пор. В гроте была установлена мраморная доска со стихами купца Ильи Васильевича Алексеева, посвящёнными поэту:

«Под сению твоей он часто находил

Приют для сладкого мечтанья,

И ты один свидетель был

Его сердечного страданья…»

Алексеев на собственные средства восстановил грот и отреставрировал дорожку к нему.

Мраморную табличку со стихами Алексеева постоянно исписывали вандалы. Люди во все времена одинаковы: одни умеют делать добро, другие – только пакостить. В 1878 году на гроте была установлена железная решётка, а внутри – бюст Лермонтова. Сейчас его нет.

Решётка на Гроте Лермонтова

Считается, что этот грот упоминается в лермонтовском романе «Герой нашего времени». Именно здесь встретились Печорин и Вера:

Хотя знатоки истории Пятигорска утверждают, что в книге описан другой грот, ныне полуразрушенный.

Самым интересным и бесспорным фактом является то, что в знаменитом фильме «12 стульев» ещё более знаменитого Леонида Гайдая Грот Лермонтова играл роль Провала.

Роль Провала в фильме «12 стульев» исполнял Грот Лермонтова

Да-да, в этом фильме Остап Бендер (его роль исполнял Арчил Гомиашвили) стоял у грота Лермонтова… и продавал билеты в Провал.

Остап Бендер продаёт билеты у входа в Провал. Сцена из кинофильма «12 стульев» режиссёра Л. Гайдая

Бендер по своей привычке и тут надул публику. Но мы-то знаем, как выглядит Провал…

А на самом деле Провал выглядит так

И Остап Бендер с билетиками там тоже стоит…

Говорят, причина была в режиссёре. Чем-то ему не угодил вид на Провал. Он посчитал, что его состояние не вполне соответствует эпохе. Хотя с исторической точки зрения, конечно, правильно было бы снимать эту сцену там.

Кстати, Гайдай сам лично выезжал в командировки на Кавминводы в поисках мест для съёмок своего будущего фильма. И нашёл подходящие места не с первого раза. Может, ему просто нравилось сюда приезжать?

Грот Лермонтова в роли Провала. Сцена из кинофильма «12 стульев» режиссёра Л. Гайдая

Ещё интересный факт. Грот Лермонтова, в отличие от Провала, совсем крошечный. Там много людей одновременно никак поместиться не могут. Именно поэтому в гайдаевском фильме в сцене с «Провалом», куда постоянно входят и откуда выходят люди, всё время меняется ракурс съёмки.

Сцена с милиционерами из кинофильма «12 стульев» режиссёра Л. Гайдая (1971 год)

Сейчас грот Лермонтова пустует. Внутри нет ни бюста поэта, ни мраморной доски со стихами, ни цветов… Остался только каменный выступ, на котором когда-то сидел Лермонтов. А весь пол усыпан монетками, которые кидают отдыхающие в надежде вернуться сюда.

Грот Лермонтова внутри с высеченной в скале скамьёй

На табличке над гротом по-прежнему расписываются вандалы. Вероятно, надеясь тем самым войти в историю города, ведь это – одна из самых известных достопримечательностей Пятигорска, очень посещаемая.

Грустно. Такое красивое историческое место. Но всегда найдётся ничтожество, которому мало просто полюбоваться…

Как найти грот Лермонтова в Пятигорске. Находится в Емануелевском парке, ниже Эоловой арфы и выше Академической галереи.

Координаты: 44.04001, 43.08721. От места, где стоит Киса Воробьянинов в Цветнике до грота рукой подать, минут 10-15 неспешной ходьбы.

Если идёте снизу, по проспекту Кирова или Красноармейской улице, то сперва увидите Академическую галерею, а от неё надо подняться по ступенькам и повернуть налево (ещё дальше наверху стоит Эолова арфа, её тоже отлично видно снизу).

Пятигорск, Емануелевский парк. Лестница вверх от Академической галереи

Если идти от домика Лермонтова, то по улице Лермонтова, она и выведет к гроту.

Можно добраться и на автобусе № 1 до Верхней радоновой лечебницы, но по Пятигорску всё же лучше гулять пешком.

Надеюсь, когда Вы будете в этих краях, то тоже прогуляетесь сюда и посмотрите, какие виды вдохновляли знаменитого поэта. А, может быть, Вы уже гуляли по этим красивейшим местам…

Вам понравился грот Лермонтова?

Все материалы сайта «Дороги мира» — авторские. Большая просьба не брать статьи и фотографии без разрешения автора и администрации сайта.

© Галина Шефер, сайт «Дороги мира», 2015. Копирование текста и фото запрещено. Все права защищены.

——————

Схожие записи:

Главные достопримечательности Пятигорска

Музей Лермонтова в Пятигорске

Канатная дорога на вершину Машука

На вершине горы Машук

Скульптура орла в Пятигорске — символ Кавминвод

Свято-Успенский Второафонский монастырь Бештау

Путешествие по Кавминводам: Пятигорск, Ессентуки, Железноводск

Спасибо, что поделились ссылкой на этот пост в соцсетях! Это помогает сайту развиваться!

КОСАГОВСКИЙ И ГРИГОРЬЕВА-СЕМЯТИЦКАЯ В ЯСНОЙ ПОЛЯНЕ * программа «Сад гениев» Международный Арт-Фестиваль

VI Международный арт-фестиваль «Сад гениев» 

АХ КАКИЕ ЛИЦА БЫЛИ НА празднике ОТКРЫТИЯ ВЫСТАВКИ — 
РОНДИЗМ В ЯСНОЙ ПОЛЯНЕ * РАЗГАДЫВАЯ ЛЕРМОНТОВА

Гением в данном случае увы организаторы имели в виду не меня а Лермонтова вероятно — но это не повод огорчаться только что опубликовал видео по открытию выставки моей  РОНДИЗМ В ЯСНОЙ ПОЛЯНЕ * РАЗГАДЫВАЯ ЛЕРМОНТОВА- на открытии были произнесены слова прощания и с легендарной Екатериной Гениевой чей проект мы и осуществляли в ее программе «Сад гениев» выставляя свои картины в музее «Ясная Поляна» графа Льва Толстого.

Два слова памяти Екатерины Гениевой — это была необычайная умница — у нее было звание — Вице-президент Международной Федерации Библиотек и получила награждения от всех ведущих стран планеты —  России, Франции, Германии, Японии и т.д. и в эстетическом мышлении она удивительно изобретательно связала шотландскую решетку с рондизмом выступая на выставке «Разгадывая Лермонтова» во Всероссийской Библиотеке Иностранной Литературы в Москве.

Конечно я объяснял и в чем суть рондизма 
(рисования кругами живописных картин) 
как мне пришла случайно эта идея открывшая новую страницу 
в мировой живописи — продолжая пуантилизм абстракционизм —
и сюрреализм — округлыми новациями — рондизма.

  На этот раз не было ф-но и импровизаций на темы зрителей но я рассказывал об этом жанре и читал стихи на другой день открывала свою выставку оригинальной живописи
в технике рваной бумаги и
Людмила Григорьева-Семятицкая 

— ее картины отличаются поэтичной недосказанностью и обобщениями пластическими и тонкой глубокой остротой иногда ракурсов

— в частности мне понравился ракурс лица Демона и Мцыри
на этом видео — само открытие выставки

….

В ЦЕНТРЕ в черном Юлия ВРОНСКАЯ — ГЛАВНЫЙ ЧЕЛОВЕК с которым имели дело все участники ФЕСТИВАЛЯ

афиша прошлой выставки

в Долине Дагестана

«Дайте мне сиянье дня…»

«Зачем я не птица…»

Демон

Мцыри

«мой дом везде где есть небесный свод. ..»

-=-

я никогда не писал абстракции  но в тот момент когда я думал о Лермонтове мне позвонил приятель заказал абстракции для выставки — но я не мог оторваться от внутренней темы да и мне было любопытно — можно ли темы эти воплотить и в абстракции — даже любопытно было как это получится… 

нежная песнь Демона

взгляд Демона

персонажи Демона

предчувствие Демона

«настанет год…»

моя душа как кубок яда

сущность фильма на Tumblr

Детали фильма — это серия сообщений в блоге, посвященных конкретным деталям фильма. Детали могут варьироваться от отдельного кадра, определенного фрагмента или фрагмента звука до отдельных сцен, объектов и других элементов мизансцены, а также более масштабных мотивов в исследуемом фильме.

Один из самых запоминающихся кадров фильма «Красные башмачки » (1948), завораживающей классики басен и балетного кино, на самом деле представляет собой тонкое сочетание двух одинаковых кадров с помощью почти незаметного перехода. это образ Ноги Мойры Ширер , когда она быстро сбегает по узкой винтовой лестнице. Кадры сделаны в довольно мелком масштабе и оформлены таким образом, что остальная часть тела персонажа обрезана, так что внимание отчетливо приковано к сияющим красным туфлям на ногах Ширера. Но важен и фон, или, конечно, не просто фон, а пространство, в котором происходит это событие: лестница. Директор Майкл Пауэлл объяснил, как он добился этого трюка вместе со своей командой.   Чтобы запечатлеть быстро движущиеся ноги актрисы, им пришлось сначала заказать отдельную винтовую лестницу для перемещения и видеосъемки, затем сделать вращающееся крепление под лестницей, чтобы можно было двигать винтовую лестницу синхронно с движение камеры вниз по крану без потери актрисы за края лестницы [1]. Впечатление безупречное и манящее. Существует загадочное ощущение движения, которое кажется невозможным, что странным образом напоминает впечатление от просмотра столь же очаровательного, хотя и совершенно другого трюкового снимка лестницы в Хичкок Головокружение (1958). Что должно привлечь особое внимание к лестнице в этот решающий момент в «Красные туфли », так это то, что это не первый случай промежуточного пространства перехода в фильме. На пути много шагов.

Перед компиляцией, анализом и интерпретацией множества ступенек Красные туфли важно кратко напомнить основную сюжетную линию фильма. Крайне важно помнить об этом, потому что именно история и основные отношения персонажей представляют ключевую тему фильма, которая артикулируется и структурируется мотивом лестницы.

Красные башмачки — фильм о конфликтах жизни и искусства. В нем рассказывается история молодой честолюбивой танцовщицы Вики Пейдж, которую играет Ширер, которую нанял Борис Лермонтов, которого играет Антон Уолбрук , в свою известную балетную труппу. Пока Вики нанята, Лермонтов также нанимает подающего надежды композитора по имени Джулиан Крастер, которого играет Мариус Геринг . Вместе они добиваются больших успехов как в творческом, так и в финансовом плане, когда Лермонтов ставит балет по мотивам Сказка Ганса Христиана Андерсена Красные туфли с Вики в главной роли и музыкой Джулиана. Однако, к большому разочарованию Лермонтова, поскольку он считает другие вещи, помимо искусства, разрушительными для творческого предприятия, Джулиан и Вики в конечном итоге влюбляются друг в друга. Лермонтов увольняет их обоих в надежде, что Вики оставит романтическую любовь и вернется к соблазну красных туфель и балета, как она в конце концов и делает. Тем не менее, Вики по-прежнему разрывается между двумя мужчинами, которые представляют ее противоречивые стремления к любви и искусству, и в конце концов умирает, попав под поезд. Она, как и главный герой сказки Андерсена, не может снять свои красные туфли; она не в состоянии избавиться от своей пагубной страсти к искусству. Рассказ довольно простой, но его возвышает искусно обработанный интертекст повести Андерсена. Тема стара как мир, но Майкл Пауэлл и Emeric Pressburger  создайте уникальный кинематографический дискурс, чтобы сформулировать тему и придать ей новый смысл. Более того, фильм изобилует деталями, создающими именно этот эффект. Мотив лестницы – один из них.

В фильме много лестниц. На балконе есть лестница, к которой бежит Вики и с которой она падает насмерть, оставив позади стремительный спуск к винтовой лестнице. Эти ступени на балконе (а не винтовая лестница) и есть настоящая последняя лестница фильма. Ближе к началу фильма есть также почти закадровая лестница, ведущая на вечеринку, устроенную тетей Вики в надежде привлечь внимание Лермонтова к ее племяннице, начинающей танцовщице. Есть закулисная лестница, ведущая на сцену в Ковент-Гарден, куда Джулиан идет после того, как Лермонтов нанял его для балета Лермонтова. Есть дальнейшие шаги, которые Юлиан поднимается с Ириной Боронской, ведущей солисткой Балета Лермонтова, которая в конечном итоге покидает труппу из-за своего замужества (показывая, чего Лермонтов опасается за Вики). За сценой есть лестница, по которой танцоры, в том числе Вики, спускаются после окончания первого класса. Ближе к концу есть подземная лестница, ведущая к платформе на вокзале, по которой Лермонтов поднимается, чтобы добраться до своего поезда, только чтобы обнаружить, что Вики пытается убедить его, что в ее жизни есть место для чего-то большего, чем просто танцы.

Все эти сцены более или менее явно касаются движения между внешним миром реальной жизни и миром грез искусства. Ниже я подробно изложу эту интерпретацию. Возможно, это более прямолинейно в сценах, где персонажи перемещаются по лестнице на сцену или от нее, и, возможно, менее явно в таких сценах, как прибытие Лермонтова на вечеринку к тете Вики или его прибытие на платформу поезда. Но тем не менее оно есть: уверенная походка Лермонтова по лестнице предшествует попытке Вики примирить конфликт; она пытается заставить Лермонтова согласиться позволить ей танцевать, а также жить своей личной жизнью.

Однако одна сцена, не упомянутая выше, особенно характерна для этой тематической функции мотива лестницы. В первый день, когда Вики и Джулиан работают в балете «Лермонтов», Лермонтов поднимается по маленькой лестнице театра из зрительного зала на сцену. Этот момент, хотя и кажущийся незначительным, особенно если рассматривать его в контексте мотива лестницы, показательен с точки зрения тематической функции лестницы в фильме. В большом кадре Лермонтов сначала проходит мимо Джулиана, пытающегося связаться с ним в зале, а затем Вики пытается связаться с ним на сцене. Лермонтов переходит из тени, то есть реального мира, в свет софитов сцены, в мир грез искусства. Именно это движение между этими двумя мирами отражено многочисленными лестницами 9-го века.0004 Красные туфли .

Все лестницы, упомянутые выше, довольно мелкие. То есть на них не обращают особого внимания, если специально их не искать. Даже только что изложенная тематическая функция может сначала показаться немного расплывчатой. Но я полагаю, что это становится более заметным, когда смотришь на эти случаи в более широком контексте мотива лестницы с его наиболее важным проявлением. Чтобы быть более конкретным, в Красные туфли есть три сцены, в которых лестницы приобретают все большее значение: это входная лестница Ковент-Гарден в начале, лестница похожего на замок здания в середине и лестница в конец (винтовая лестница и лестница на балкон). Поскольку я уже описал финальную сцену с винтовой лестницей и лестницей на балконе, я начну с описания начальной и средней сцен, которые не были упомянуты выше.

Лестница в начале — первое, что мы видим в фильме. Фильм начинается с кадра ведущей вверх лестницы под низким углом. На звуковой дорожке слышен закадровый шум толпы со стороны. Портье входит в пространство экрана наверху лестницы и спускается на несколько ступенек. Кадр показывает двух охранников, которые держат закрытую дверь под лестницей. Портье говорит им открыть двери и впустить ожидающую толпу. Толпа — это группа возбужденных студентов, которые вот-вот сойдут с ума из-за балета. Открытие балета Лермонтова в Ковент-Гарден. Камера следит за интенсивным бегом студентов по лестнице, пока не останавливается в углу, чтобы запечатлеть их восторженные движения, которые даже заканчиваются тем, что рвут на стене афишу «Балета Лермонтова» к спектаклю. Реальный мир, оставшийся позади, тактильный, осязаемый, тогда как мир искусства совсем не такой. Аудитория здесь, чтобы сидеть на месте; они там до видят и к слышат , так как они очень четко подчеркивают в диалоге друг с другом. Именно эта вступительная сцена устанавливает тему движения между двумя мирами через мотив лестницы.

Между сценой с лестницей в начале и сценой с лестницей в конце (как с винтовой лестницей, так и с лестницей на балконе) соответственно есть еще одна главная сцена с лестницей в середине фильма. Это сцена, где Вики, одетая в красивое синее платье с очаровательной тиарой, подчеркивающей ее рыжие волосы великолепным цветом Technicolor, вызывается Лермонтовым в его компанию в жутком замке, похожем на здание прямо со страниц сказки. -сказка. Прибыв на место, она поднимается по лестнице и находит массивные ступени, покрытые травой. Наверху есть еще лестницы, по которым нужно подняться. И что ее ждет после всех этих шагов? Лермонтов говорит ей, что она будет играть главную роль в его новом балете по сказке Ганса Христиана Андерсена Красные туфли .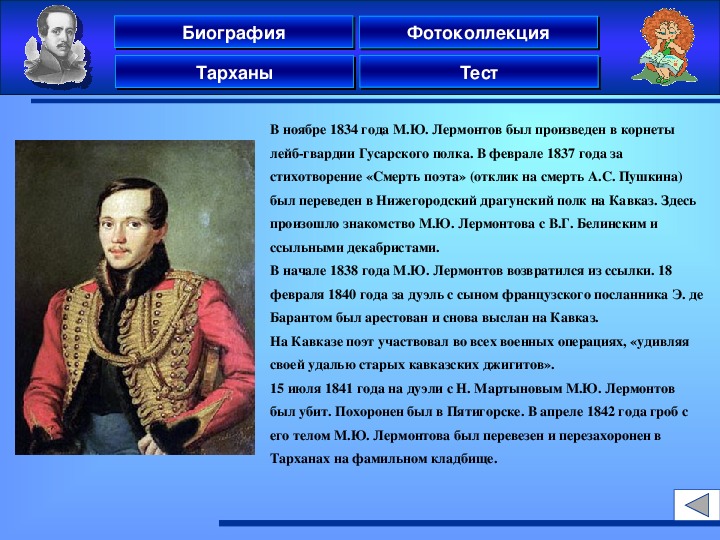 Длина перехода от земли к более высокой вершине, где ждет Лермонтова, кажется, отражает трудности, с которыми сталкивается вхождение в жизнь искусства. Однако в то же время продолжительность пути к вершине выражает оторванность мира искусства от реального мира внизу. Кроме того, длинная лестница, покрытая травой, таит в себе загадку, усиливая переход в сказочный мир искусства. Создается впечатление, что фильм взял краткую паузу, чтобы подчеркнуть не только повествовательную важность этого поворотного момента, но и очарование искусства, которое одновременно заманчиво и ужасающе.

Как уже было сказано, лестницы в этих трех сценах более заметны. Они артикулируют, возможно, более явно тему движения между реальным миром и миром грез искусства. В начальной сцене возбужденные студенты мчатся по лестнице, оставляя тактильный реальный мир позади, чтобы приблизиться к мечте. Джулиан Крастер, композитор, которого Лермонтов в конце концов нанимает для своей труппы и в которого Вики влюбляется, сидит на балконе и слушает музыку. Вики, однако, ближе к сцене; она уже очарована, может быть, даже слишком очарована миром грез искусства. Именно она говорит Лермонтову, что то, как другие оправдывают продолжение жизни, она оправдывает танцами. Для нее смысл существования человека эквивалентен смыслу существования танца. И, конечно же, именно она умирает за это. В упомянутой чуть выше сцене, где Вики поднимается по высокой лестнице похожего на замок здания, чтобы услышать сообщение Лермонтова, изменившее ее жизнь, присутствует похожее ощущение межмирового движения. Вики одета как принцесса, но не для этого случая, который стал для нее неожиданностью; она поднимается по заросшей травой лестнице в замок; она узнает, что будет играть главную роль в балете по басне. Коннотация сказки как нельзя более однозначна. Реальный мир остается позади, а персонаж поднимается (тоже конкретно по длинной лестнице) в духовный план искусства. Эстетика сказки используется для того, чтобы еще больше подчеркнуть оторванность мира искусства от реального мира, оторванность, как говорится, и соблазнительную, и пугающую.

В обеих этих сценах персонажи приближаются к сфере искусства. В отличие от них знаменитый образ Вики, быстро бегущей по винтовой лестнице, передает противоположное движение. Это делается не только для того, чтобы указать на тот простой факт, что люди бегут или идут с 90 004 на 90 005 в первой и средней сценах, тогда как Вики бежит с 90 004 на 90 005 в последней сцене, но и для того, чтобы сделать метафорическое наблюдение об этих видах движения. . Словом, стремительный бег Вики — это бегство от мечты (своей мечты), а не приближение к ней. После сцены, где ее практически разрывают на части Лермонтов и Джулиан, первый из которых олицетворяет фантастический мир искусства, а второй — реальный мир с романтическими отношениями, Вики охватывает чувство ужаса, когда она, шатаясь, идет к сцене в сопровождении костюмера. . Она — возможно, управляемая красными туфлями, как девочка в сказке Андерсена — начинает отдаляться. Она убегает и мчится к винтовой лестнице. Образ ее ног, бегущих по лестнице, представляет ее страх, ее неконтролируемую потребность и ее противоречивое желание уйти подальше от мира грез искусства, который значит для нее все, но также и ее противоречивое желание не уходить. мир искусства, который начал ее поглощать. Неясность того, что на самом деле происходит в этом финале (свободная воля Вики или чары красных туфель? Вики бежит обратно к своей любви или бежит навстречу смерти?) подчеркивает неразрешенный конфликт искусства и жизнь, которая мучает главного героя.

В отличие от других лестниц в фильме, винтовая лестница поражает своим сюрреалистичным размером. Когда в фильме видишь лестницы, то совершенно уверен в их расположении и пространственной связи с другими помещениями. В этом нет ничего удивительного, ведь лестница как раз и является связующим звеном между двумя или более помещениями, как правило, между этажами. Могут быть четкие визуальные подсказки, такие как знак стрелки и слово «этап» на стене, напоминающие нам, куда ведет лестница, или переходы от предыдущих сцен к последующим сценам, которые обеспечивают пространственный контекст для лестницы. Так обстоит дело, например, со сценой, где Вики тренируется с другими танцорами труппы. Сцена заканчивается тем, что хореограф кричит: «Урок уволен!» Кадр переносит нас к лестнице за кулисами, по которой спускается Вики (см. изображение выше). На заднем плане на стене видно слово «сцена». Камера следует за Вики, которая отходит все дальше от сцены, пока камера не останавливается в музыкальной репетиционной комнате, куда нас переносит следующий фрагмент. В качестве другого примера возьмем сцену с похожим на замок зданием. Таксист забирает Вики из отеля. Долгая поездка приводит ее в неизвестное место, но кадры красивой природы дают зрителю пространственно связное ощущение путешествия. После поездки Вики появляется в начале первой лестницы, по которой она начинает подниматься; затем переход к движению перемещает нас к ее прибытию на вершину этой лестницы, где она открывает ворота, в подвижном следующем кадре, к огромному лестничному пролету, покрытому травой. Наконец, растворение показывает, как она поднимается на вершину еще одной лестницы, которая в конечном итоге приводит ее к Лермонтову. В обеих сценах пространственные отношения очень четкие. Для изображения винтовой лестницы таких реплик нет.

После кадра, в котором Вики в страхе убегает, появляется кадр, где дирижер оркестра начинает балет «Красные башмачки». Следующие кадры переносят нас к винтовой лестнице, точное местонахождение которой в здании остается загадкой. Следующий кадр также не помогает создать контекст для пространственных отношений: камера остается на ногах Вики в красных туфлях, остальная часть ее тела обрезана, она идет по неизвестному коридору и спускается на несколько ступенек, пока не подходит к лестнице. на балконе, которые ведут в более привычное пространство балкона над железнодорожными путями. В дополнение к кадрам, предшествующим и следующим за двумя комбинированными планами винтовой лестницы, кадры самой винтовой лестницы еще больше усиливают пространственную двусмысленность. Учитывая скорость бегства Вики и продолжительность двух выстрелов, можно было бы предположить, что винтовая лестница покрывала довольно долгое путешествие. Трудно представить, где именно в здании располагалась бы такая большая винтовая лестница. Можно, конечно, но как-то непонятно. Это сюрприз для зрителя, и в этом сюрпризе как раз и дело.

Более важным, чем кадры, окружающие изображение бега по винтовой лестнице, является, конечно, общее жуткое впечатление от изображения самой винтовой лестницы. Сочетая быстрое движение актрисы с синхронизированным движением камеры, а также с незаметным движением винтовой лестницы, изображение приобретает совершенно уникальное ощущение, которое довольно сложно передать словами. Тот факт, что реальная лестница в физическом пространстве (студийной обстановке) была перемещена с помощью вращающегося крепления во время съемок, позволяет камере запечатлеть движение актрисы иначе, чем если бы лестница оставалась неподвижной. Однако, поскольку лестница не движется в диегетическом пространстве (т. е. пространстве вымышленного мира, где действуют персонажи), зрительное впечатление, мягко говоря, озадачивает. Это только подчеркивает фактор неожиданности перехода к винтовой лестнице. Сюрреализм образа подчеркивает, что бегство главного героя на самом деле не физическое или конкретное, а метафорическое. В поэтическом пространстве фильма героиня отрывается от мира грез искусства, который для нее значит все, от мира, чья оторванность от реальности была установлена ​​не позднее чем баснословной лестницей, поросшей травой. Неразрешенный конфликт может закончиться только смертью.

В дополнение к тематической траектории, намеченной этими тремя сценами (первые шаги в мир искусства в Ковент-Гарден в начале, затем вход в этот мир по лестнице, покрытой травой в середине, и, наконец, бегство от его потребления души в винтовой лестнице в конце), стоит отметить, что в знаменитом семнадцатиминутном балетном эпизоде ​​фильма тоже есть лестница. То есть лестницы в значительной степени задействованы в производственном дизайне не только Пауэлла и Прессбургера.0004 «Красные башмачки» , но и в «Красных башмачках» балета Лермонтова. На заднем плане основной сцены балета есть лестница, по которой сначала поднимаются и спускаются две женщины. В конце концов, девушка в красных туфлях, которую играет Вики, падает на лестнице после того, как устала от красных туфель. Освободившись от проклятия красных туфель смертью, тело Вики, наконец, несет мужчина к лестнице.

Хотя такое использование мотива лестницы имеет место в рассказе внутри рассказа (история Андерсена как балет в исполнении персонажей фильма), довольно интересно, что лестницы появляются в начале и в конце балета, просто как в самом фильме. Лестница в балете также означает переход и, в частности, смерть. Словно лестница, ассоциирующаяся в первую очередь с входом и движением, со временем превратилась в ворота между двумя мирами. Вики сначала попадает в мир искусства (первый экземпляр лестницы в балете), затем умирает за него и, наконец, уносится из него обратно в реальность (последний экземпляр лестницы в балете). Такая близость балета и фильма, конечно, не должна вызывать удивления. Ибо балет в очень большой степени отражает многие события фильма, в том числе и назревающий конфликт Вики между Юлианом и Лермонтовым.

Лестница — это промежуточное пространство между помещениями. Таким образом, движение по лестнице обычно означает переход. Здесь я утверждал, что лестница в «Красные туфли » работает как метафора движения персонажей (в основном Вики) между реальным миром жизни и миром искусства грез. Движение часто случайное, но даже тогда оно иллюстрирует эту тематическую функцию. В сценах, где движение менее случайно, а лестница более заметна, то есть в трех сценах в начале, середине и конце, о которых говорилось выше, артикуляция и структурирование этой темы более заметны. Вики сначала влечет к миру грез его таинственная приманка в первой и второй из этих сцен, устанавливающих оторванность мира грез от реальности, но в конце концов она почти отталкивается от мира грез это даже ужасное очарование, с которым она когда-то так сильно отождествляла себя. В удивительных кадрах винтовой лестницы связь между мирами оборвалась, что отражается в жутком движении в кадрах и двойственности отношений с другими пространствами. Образ шокирует. Необычайный эффект образа бега по винтовой лестнице, пространственной связи одновременно смещенной и сверхъестественной, выражает этот неоднозначный и неразрешенный конфликт искусства и жизни в жизни художника.

Примечания:

[1] Майкл Пауэлл рассказывает этот анекдот Питеру фон Багу на кинофестивале «Полуночное солнце» в 1987 году: «В конце фильма, когда девушка бежит насмерть в красных туфлях, она выходит из раздевалки. Я подумал, что было бы ужасно скучно, если бы она просто спускалась по лестнице обычным способом, поэтому я сделал для сцены винтовую лестницу примерно шести метров, подобные которой используются на промышленных объектах. Я спросила Мойру, может ли она спуститься по лестнице в своих балетках. Она сказала мне, что может. Камера должна была снимать бег от опускающегося крана. Я попросил Мойру бежать как можно быстрее, потому что хотел, чтобы кадр был как можно короче. Я дал Мойре сигнал идти, и она побежала вниз по лестнице быстрее, чем могла уследить камера. Она опередила камеру примерно на 20 кадров. Кинематографистам было стыдно. Ей пришлось снова бежать, и на этот раз камера не отставала от нее, но когда Мойра бежала по винтовой лестнице, она, конечно, на мгновение закрывалась лестницей на каждом круге. Так как камера не могла вращаться вокруг лестницы с той же скоростью, нам пришлось сделать для лестницы вращающееся крепление, скорость которого можно было бы регулировать, чтобы Мойра постоянно находилась перед камерой. Мы сказали Мойре, что теперь она может бегать так быстро, как хочет. Она побежала и снова выиграла камеру на две секунды. Позже, когда мы сделали кадр, мой редактор Реджи Миллс спросил меня, можем ли мы удлинить лестницу. Я ответил, что нет, если только мы не получим новую лестницу. Но кадр был слишком коротким, поэтому мы решили проявить его дважды, а затем соединить части так, чтобы это выглядело как один кадр». (Peter von Bagh, Sodankylä ikuisesti [ Sodankylä Forever ], WSOY, 2010, стр. 55; мой перевод с финского текста.)