Как посчитать эволюцию: Рассчитать дату овуляции — «Айвимед»
Наука против старости. Как разогнать эволюцию и быть вечно молодым
Существуют животные, которых можно назвать эволюционными чемпионами. Они просто отключили старение и могут сохранять молодой организм всю жизнь
В двух предыдущих сериях нашего био-сериала я попытался подвести читателя к мысли, что старение и венчающее его смерть не являются какими-то случайными процессами, происходящими из-за несовершенства устройства нашего организма, его изнашивания. На мой взгляд, более правильно рассматривать их как финальную стадию программы развития индивида, заложенную, как и все остальные стадии, в наши гены. В этой статье я постараюсь привести вам важнейший аргумент, подтверждающий, что это действительно так.
Жизнь без старости
Для начала позволю себе небольшое отступление. А зачем вообще может понадобиться такая неприятная штука, как старение? Ну ладно еще — просто смерть. Она необходима для смены поколений. Но с какой стати природа наградила нас унизительным периодом увядания жизненных функций? Неужели нельзя было обойтись без него и просто жить себе — не тужить и умирать в один день?
А зачем вообще может понадобиться такая неприятная штука, как старение? Ну ладно еще — просто смерть. Она необходима для смены поколений. Но с какой стати природа наградила нас унизительным периодом увядания жизненных функций? Неужели нельзя было обойтись без него и просто жить себе — не тужить и умирать в один день?
Короткий ответ — обойтись без старения можно!
Оказывается, есть виды животных, причем среди них есть и наши близкие родственники — млекопитающие, у которых старения практически нет. На самом деле, похоже, таких видов довольно много. Но только один изучается в лабораториях. Знакомьтесь, тотемный зверь нашего проекта по борьбе со старением — голый землекоп. На самом деле это грызун, т.е. родственник мыши, примерно такого же размера:
Так вот, исходя из его размеров, скорости метаболизма, положения в классификации животных, он должен был бы жить примерно как мышь или крыса — 2,3 ну максимум 5 лет. А он живет… неизвестно сколько. Эксперимент идет уже более 30 лет и до сих живы землекопы, которые были отловлены в Африке более 30 лет назад. И что самое главное , смертность землекопов не растет с возрастом. То есть что 2-х летние, что 10-летние, что 20-летние зверьки празднуют свой следующий день рождения с одинаковой вероятностью. То есть они, просто по определению, не стареют.
Возникают два разумных вопроса:
- Почему голому землекопу так повезло?
- Как, во имя Дарвина и Вейсмана, он это сделал?!
В этой статье я постараюсь ответить на первый вопрос.
Мудрая старость
Для этого сначала придется изложить точку зрения, что старение это еще один способ ускорения эволюции. Такой же как половое размножение и смерть (см. первую серию нашего сериала). Дело в том, что главной движущей силе эволюции — естественному отбору — обычно гораздо удобнее работать не на молодых и здоровых животных, а на слегка ослабленных особях. То есть стариках. А именно их и изготавливает старение.
- Отменить смерть. Может ли человек бросить вызов своим генам
Отмечу, что в дикой природе понятие «старик» сильно отличается от нашего, человеческого. В первую очередь потому что у животных нет менопаузы. То есть, какими бы «старыми» они не были, они все равно могут размножаться. Старение же проявляется в ослаблении общей функциональности организма и, как следствие, повышает вероятность смерти.
Для наглядной иллюстрации этого соображения академик Владимир Скулачев как-то придумал специальную «теорему о двух зайцах». Вот она: представьте себе двух зайцев. Для простоты допустим, что главным фактором естественного отбора означенных зайцев является лиса — съест она их или нет. Теперь предположим, что один из зайцев несет в своих генах небольшую (единичную), но немножко полезную мутацию. Ну, например он чуть-чуть умнее остальных своих сородичей. Но именно чуть-чуть — ведь крайне маловероятно, чтобы в результате одной мутации он стал сразу заячьим Эйнштейном. С точки зрения развития вида ушастых любителей морковки, было бы очень правильно дать какое-то преимущество именно умному зайцу, чтобы попытаться закрепить этот полезный признак в будущих поколениях. Но как это сделать, если признак очень маленький и для естественного отбора крайне незначителен? Другими словами, и обычный и «умный» зайцы одинаково хорошо убегают от лисы («Заяц всегда убежит от лисы, потому что для него это вопрос жизни и смерти, а для нее — обеда», — говорил Эзоп»). Но давайте запустим у наших зайцев старение. Начнем потихоньку ухудшать работу всех систем. Они начинают медленнее бегать, хуже путать следы, вот уже и сердечко пошаливает, и болеют они чаще из-за ослабленной иммунной системы. С такими слегка состарившимися зайцами у лисы в некоторый момент уже появляются хорошие шансы их догнать и съесть.
Но давайте запустим у наших зайцев старение. Начнем потихоньку ухудшать работу всех систем. Они начинают медленнее бегать, хуже путать следы, вот уже и сердечко пошаливает, и болеют они чаще из-за ослабленной иммунной системы. С такими слегка состарившимися зайцами у лисы в некоторый момент уже появляются хорошие шансы их догнать и съесть.
Кстати, хищники на самом деле как правило питаются старыми и больными животными, а не молодыми и здоровыми. Из фото охоты львов на буйволов видно, что, попытайся хищники атаковать стадо молодых животных, соотношение сил было бы совсем не в пользу львов.
Но в отношении умного зайца такие шансы «быть съеденным» появятся позже, потому что поначалу его «умность» позволит ему убегать от лисы, даже несмотря на общее ослабление от старения. Например, он чуть лучше путает следы или раньше засекает хищника. В результате появляется период, причем довольно продолжительный, поскольку старение идет медленно, когда небольшое преимущество в скорости обработки информации будет спасать ему жизнь. Все это время будут съедать не его, а обычных зайцев. Как следствие умный успеет еще пару раз наплодить зайчат и, в результате, следующее поколение этого вида будет «обогащено» более умными зайцами. И произойдет это исключительно благодаря старению, которое позволило естественному отбору «вытащить из под шумов» и закрепить мелкие признаки, незаметные на фоне молодых и здоровых особей.
Все это время будут съедать не его, а обычных зайцев. Как следствие умный успеет еще пару раз наплодить зайчат и, в результате, следующее поколение этого вида будет «обогащено» более умными зайцами. И произойдет это исключительно благодаря старению, которое позволило естественному отбору «вытащить из под шумов» и закрепить мелкие признаки, незаметные на фоне молодых и здоровых особей.
Эволюционное исключение
Почему мне понадобилось это пространное отступление про зайцев? Почему важно понимать, что старение — это инструмент, ускоряющий эволюцию? Потому что это позволяет сформулировать важную гипотезу:
Существуют животные, которых можно назвать эволюционными чемпионами. Это твари, которые изобрели (разумеется, в результате эволюции) что-то такое, что позволило им потрясающе приспособиться к условиям окружающей среды и дальше их менять — только портить. Очень редко, но такие примеры найти можно. Гипотеза заключается в том, что подобные виды могут себе позволить … не стареть.
Очень редко, но такие примеры найти можно. Гипотеза заключается в том, что подобные виды могут себе позволить … не стареть.
Упомянутый выше голый землекоп — это и есть такой чемпион. Не смотрите на то, что он маленький, как бы тщедушный (совсем нет, как выяснилось), и страшноватый.
На самом деле перед вами — великий изобретатель, покруче нас, людей. Дело в том, что землекоп — это единственное эусоциальное млекопитающее. Мы с вами — квазисоциальны. То есть, если очень припрет, мы можем и парой на необитаемом острове выжить. А землекоп — нет. Они живут подобно социальным насекомым — муравьям, термитам и пчелам — колониями с четким разделением обязанностей и профессий. И только так могут существовать.
Во главе колонии стоит королева-мать. При ней есть ее муж — крон-принц. То ли один, то ли их бывает до 3-х штук, тут ученые до сих пор не разобрались. Колония может насчитывать от пары десятков до нескольких сотен подданных королевы. Причем большинство из них — ее дети. Размножаться может только королева. Остальные — это охранники, солдаты, рабочие, фуражиры, няньки и т.д. Живут они под землей в очень твердом грунте в восточной Африке. При такой матриархальной системе для эволюции имеют значение только королева и ее муж (мужья). Потому что только они приносят потомство, т.е. передают свои гены в следующее поколение. Остальная колония — это обслуживающий персонал. Понятно, что при таком устройстве никаких особых проблем с приспособлением к окружающей среде у королевской четы нет. Их кормят, оберегают, стоят им удобные покои в центре лабиринта. Что бы не происходило там, на поверхности, им ни к чему приспосабливаться особенно не нужно. А значит можно позволить себе, например, эволюционировать в каком-то более расслабленном режиме. А для этого стоило бы отключить какие-то особенно «хлопотные» механизмы ускорения эволюции — например, старение.
Колония может насчитывать от пары десятков до нескольких сотен подданных королевы. Причем большинство из них — ее дети. Размножаться может только королева. Остальные — это охранники, солдаты, рабочие, фуражиры, няньки и т.д. Живут они под землей в очень твердом грунте в восточной Африке. При такой матриархальной системе для эволюции имеют значение только королева и ее муж (мужья). Потому что только они приносят потомство, т.е. передают свои гены в следующее поколение. Остальная колония — это обслуживающий персонал. Понятно, что при таком устройстве никаких особых проблем с приспособлением к окружающей среде у королевской четы нет. Их кормят, оберегают, стоят им удобные покои в центре лабиринта. Что бы не происходило там, на поверхности, им ни к чему приспосабливаться особенно не нужно. А значит можно позволить себе, например, эволюционировать в каком-то более расслабленном режиме. А для этого стоило бы отключить какие-то особенно «хлопотные» механизмы ускорения эволюции — например, старение.
И землекоп действительно отключил себе старение. Лучше всего это видно по графику зависимости смертности землекопов от возраста. Ее (зависимость) удалось посчитать по результатам эпического эксперимента, который в течение 25 лет вела американский зоолог Рашель Баффенстайн. Вот ее статье 2005 года на рисунке номер 5 приведен этот график:
На графике показана смертность голых землекопов в зависимости от возраста·The Journals of Gerontology
Видите — это же горизонтальная линия! То есть вероятность смерти у землекопов в любом возрасте… одинаковая! У нас с вами, да и у любых других стареющих животных эта вероятность растет по экспоненте (смотри график ниже). А у землекопов — нет.
Смертность людей в зависимости от возраста·По данным федеральной службы государственной статистики за 2010 год
График смертности землекопов наделал много шума в научном сообществе 12 лет назад. Все бросились изучать этих зверьков и уже довольно много о них узнали. Оказалось, что это настоящие
Все бросились изучать этих зверьков и уже довольно много о них узнали. Оказалось, что это настоящие супермены супермаусы. Они практически не чувствуют боли, их мозг выдерживает аномально долгое кислородное голодание, а с возрастом не истончаются кости и не страдают суставы, и вообще, большинство старческих болезней у них либо просто не обнаружены, либо крайне редки.
Это же касается потрясающей устойчивости землекопов к онкологическим заболеваниям. Долгое время ученым просто не удавалось обнаружить у них ни одного случая раковой опухоли. Более того, были открыты и некоторые механизмы этой устойчивости к раку — например клетки голого землекопа обладают особенно сильным т.н. «контактным торможением роста». То есть, когда клетки, подобно раковым, начинают безудержно делиться, они очень быстро соприкасаются со своими соседями. Так вот, факт такого соприкосновения для клеток землекопа приводит к очень строгому запрету на дальнейшее деление.
Справедливости ради надо сказать, что в конце концов после патоморфологического анализа 1200 трупиков голых землекопов таки удалось обнаружить пару случаев раковых опухолей. Но если бы такой анализ проводился с лабораторными мышами, то рак был бы найден почти у 100% животных. Это касается и человека : около трети умерших людей имеют раковые образования. То есть землекоп в сотни раз устойчивей к раку по сравнению с нами!
Фото МГУ
Подозреваю, что вас уже начал мучить вопрос, а как же голому землекопу удалось отключить свое старение (смотри второй вопрос в начале статьи)? Похоже, наша научная группа в этом разобралась, о чем я и расскажу в следующей колонке моей серии. Следите за продолжением!
В заключение напомню, что землекоп смог позволить себе «отключить» печальные обстоятельства, связанные со старением, просто потому что ему больше нет нужды в ускорении эволюции. И вот тут я бы хотел обратить ваше просвещенное внимание, на то, что Homo Sapiens тоже является таким «эволюционным чемпионом». В способности адаптироваться к окружающей среде мы переплюнули даже голых землекопов. Потому что используем для этого не эволюцию с ее черепашьей скоростью эволюции, а технический прогресс.
И вот тут я бы хотел обратить ваше просвещенное внимание, на то, что Homo Sapiens тоже является таким «эволюционным чемпионом». В способности адаптироваться к окружающей среде мы переплюнули даже голых землекопов. Потому что используем для этого не эволюцию с ее черепашьей скоростью эволюции, а технический прогресс.
Если нам хочется жить севернее, то мы не отращиваем мех, а изобретаем одежду. Если нам не хватает еды, мы не увеличиваем себе желудочно-кишечный тракт для переваривания травы, а создаем сельское хозяйство. То есть мы вполне заслужили звание «чемпионов». Вот только независимость от эволюции мы приобрели совсем недавно — всего несколько тысяч лет назад. А землекоп — несколько миллионов. Поэтому, может быть, мы просто еще не успели избавиться от такой мелкой эволюционной пакости как старение? Похоже, что это действительно так и я постараюсь доказать это в следующих сериях.
Также там будет поставлен и еще один важный вопрос — можно ли для отмены старения у человека не ждать миллион лет эволюции вида Homo Sapiens, а применить наш излюбленный прием — технический прогресс?
Генетические алгоритмы — математический аппарат
Генетические алгоритмы предназначены для решения задач оптимизации и моделирования путём последовательного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию.
Генетические алгоритмы предназначены для решения задач оптимизации. Примером подобной задачи может служить обучение нейросети, то есть подбора таких значений весов, при которых достигается минимальная ошибка. При этом в основе генетического алгоритма лежит метод случайного поиска. Основным недостатком случайного поиска является то, что нам неизвестно сколько понадобится времени для решения задачи.
Для того, чтобы избежать таких расходов времени при решении задачи, применяются методы, открытые при изучении эволюции и происхождения видов. Как известно, в процессе эволюции выживают наиболее приспособленные особи. Это приводит к тому, что приспособленность популяции возрастает, позволяя ей лучше выживать в изменяющихся условиях.
Впервые подобный алгоритм был предложен в 1975 году Джоном Холландом (John Holland) в Мичиганском университете. Он получил название «репродуктивный план Холланда» и лег в основу практически всех вариантов генетических алгоритмов. Однако, перед тем, как мы его рассмотрим подробнее, необходимо остановится на том, каким образом объекты реального мира могут быть закодированы для использования в генетических алгоритмах.
Представление объектов
Из биологии мы знаем, что любой организм может быть представлен своим фенотипом, который фактически определяет, чем является объект в реальном мире, и генотипом, который содержит всю информацию об объекте на уровне хромосомного набора. При этом каждый ген, то есть элемент информации генотипа, имеет свое отражение в фенотипе.
Таким образом, для решения задач нам необходимо представить каждый признак объекта в форме, подходящей для использования в генетическом алгоритме. Все дальнейшее функционирование механизмов генетического алгоритма производится на уровне генотипа, позволяя обойтись без информации о внутренней структуре объекта, что и обуславливает его широкое применение в самых разных задачах.
В наиболее часто встречающейся разновидности генетического алгоритма для представления генотипа объекта применяются битовые строки. При этом каждому атрибуту объекта в фенотипе соответствует один ген в генотипе объекта. Ген — битовая строка, чаще всего фиксированной длины, которая представляет собой значение этого признака.
Ген — битовая строка, чаще всего фиксированной длины, которая представляет собой значение этого признака.
Кодирование признаков (целые числа)
Для кодирования таких признаков можно использовать самый простой вариант — битовое значение этого признака. Тогда нам будет весьма просто использовать ген определенной длины, достаточной для представления всех возможных значений такого признака. Но, к сожалению, такое кодирование не лишено недостатков.
Основной недостаток заключается в том, что соседние числа отличаются в значениях нескольких битов, так например числа 7 и 8 в битовом представлении различаются в 4-х позициях, что затрудняет функционирование генетического алгоритма и увеличивает время, необходимое для его сходимости. Для того, чтобы избежать эту проблему лучше использовать кодирование, при котором соседние числа отличаются меньшим количеством позиций, в идеале значением одного бита.
Таким кодом является код Грея, который целесообразно использовать в реализации генетического алгоритма. Значения кодов Грея рассмотрены в таблице ниже:
Значения кодов Грея рассмотрены в таблице ниже:
| Десятичный код | Двоичное значение | Шестнадцатеричное значение | Десятичный код | Двоичное значение | Шестнадцатеричное значение |
|---|---|---|---|---|---|
| 0 | 0000 | 0h | 0 | 0000 | 0h |
| 1 | 0001 | 1h | 1 | 0001 | 1h |
| 2 | 0010 | 2h | 3 | 0011 | 3h |
| 3 | 0011 | 3h | 2 | 0010 | 2h |
| 4 | 0100 | 4h | 6 | 0110 | 6h |
| 5 | 0101 | 5h | 7 | 0111 | 7h |
| 6 | 0110 | 6h | 5 | 0101 | 5h |
| 7 | 0111 | 7h | 4 | 0100 | 4h |
| 8 | 1000 | 8h | 12 | 1100 | Ch |
| 9 | 1001 | 9h | 13 | 1101 | Dh |
| 10 | 1010 | Ah | 15 | 1111 | Fh |
| 11 | 1011 | Bh | 14 | 1110 | Eh |
| 12 | 1100 | Ch | 10 | 1010 | Ah |
| 13 | 1101 | Dh | 11 | 1011 | Bh |
| 14 | 1110 | Eh | 9 | 1001 | 9h |
| 15 | 1111 | Fh | 8 | 1000 | 8h |
Таблица 1. Соответствие десятичных кодов (слева) и кодов Грея (справа)
Соответствие десятичных кодов (слева) и кодов Грея (справа)
Таким образом, при кодировании целочисленного признака мы разбиваем его на тетрады и каждую тетраду преобразуем по коду Грея.
В практических реализациях генетических алгоритмов обычно не возникает необходимости преобразовывать значения признака в значение гена. На практике имеет место обратная задача, когда по значению гена необходимо определить значение соответствующего ему признака.
Таким образом, задача декодирования значения генов, которым соответствуют целочисленные признаки, тривиальна.
Кодирование признаков (действительные числа)
Самый простой способ кодирования, который лежит на поверхности – использовать битовое представление, хотя такой вариант имеет те же недостатки, что и для целых чисел. Поэтому на практике обычно применяют следующую последовательность действий:
- Разбивают весь интервал допустимых значений признака на участки с требуемой точностью.
- Принимают значение гена как целочисленное число, определяющее номер интервала (используя код Грея).

- В качестве значения параметра принимают число, являющиеся серединой этого интервала.
Рассмотрим вышеописанную последовательность действий на примере.
Допустим, что значения признака лежат в интервале [0, 1]. При кодировании использовалось разбиение участка на 256 интервалов. Для кодирования их номера нам потребуется, таким образом, 8 бит. Допустим, значение гена: 00100101bG (заглавная буква G показывает, что используется кодирование по коду Грея). Для начала, используя код Грея, найдем соответствующий ему номер интервала:
25hG->36h->54d.
Теперь посмотрим, какой интервал ему соответствует… После несложных подсчетов получаем интервал [0.20703125, 0.2109375]. Значит значение нашего параметра будет (0.20703125+0.2109375)/2=0.208984375.
Кодирование нечисловых данных
При кодировании нечисловых данных необходимо предварительно преобразовать их в числа.
Определение фенотипа по генотипу
Для того чтобы определить фенотип объекта (то есть значения признаков, описывающих объект) нам необходимо только знать значения генов, соответствующим этим признакам, то есть генотип объекта. При этом совокупность генов, описывающих генотип объекта, представляет собой хромосому. В некоторых реализациях ее также называют особью.
При этом совокупность генов, описывающих генотип объекта, представляет собой хромосому. В некоторых реализациях ее также называют особью.
Таким образом, в реализации генетического алгоритма хромосома представляет собой битовую строку фиксированной длины. При этом каждому участку строки соответствует ген. Длина генов внутри хромосомы может быть одинаковой или различной. Чаще всего применяют гены одинаковой длины.
Рассмотрим пример хромосомы и интерпретации ее значения. Допустим, что у объекта имеется 5 признаков, каждый закодирован геном длинной в 4 элемента. Тогда длина хромосомы будет 5*4=20 бит:
| 0010 | 1010 | 1001 | 0100 | 1101 |
|---|
Теперь мы можем определить значения признаков:
| Признак | Значение гена | Двоичное значение признака | Десятичное значение признака |
|---|---|---|---|
| 1 | 0010 | 0011 | 3 |
| 2 | 1010 | 1100 | 12 |
| 3 | 1001 | 1110 | 14 |
| 4 | 0100 | 0111 | 7 |
| 5 | 1101 | 1001 | 9 |
Основные генетические операторы
Как известно, в теории эволюции важную роль играет то, каким образом признаки родителей передаются потомкам. В генетических алгоритмах за передачу признаков родителей потомкам отвечает оператор, который называется скрещивание (его также называют кроссовер или кроссинговер). Этот оператор определяет передачу признаков родителей потомкам.
В генетических алгоритмах за передачу признаков родителей потомкам отвечает оператор, который называется скрещивание (его также называют кроссовер или кроссинговер). Этот оператор определяет передачу признаков родителей потомкам.
Действует он следующим образом:
- из популяции выбираются две особи, которые будут родителями;
- определяется (обычно случайным образом) точка разрыва;
- потомок определяется как конкатенация части первого и второго родителя.
Рассмотрим функционирование этого оператора:
| Хромосома_1 | 0000000000 |
| Хромосома_2 | 1111111111 |
Допустим, разрыв происходит после 3-го бита хромосомы, тогда:
| Хромосома_1 | 0000000000 | >> | 000 | 1111111 | Результирующая_хромосома_1 |
| Хромосома_2 | 1111111111 | >> | 111 | 0000000 | Результирующая_хромосома_2 |
Затем с вероятностью 0. 5 определяется одна из результирующих хромосом в качестве потомка.
5 определяется одна из результирующих хромосом в качестве потомка.
Следующий генетический оператор предназначен для того, чтобы поддерживать разнообразие особей с популяции. Он называется оператором мутации. При использовании данного оператора каждый бит в хромосоме с определенной вероятностью инвертируется.
Кроме того, используется еще и так называемый оператор инверсии, который заключается в том, что хромосома делится на две части, и затем они меняются местами. Схематически это можно представить следующим образом:
| 000 | 1111111 | >> | 1111111 | 000 |
В принципе для функционирования генетического алгоритма достаточно этих двух генетических операторов, но на практике применяют еще и некоторые дополнительные операторы или модификации данных операторов.
Например, кроссовер может быть не одноточечный (как было описано выше), а многоточечный, когда формируется несколько точек разрыва (чаще всего две). Кроме того, в некоторых реализациях алгоритма оператор мутации представляет собой инверсию только одного случайно выбранного бита хромосомы.
Кроме того, в некоторых реализациях алгоритма оператор мутации представляет собой инверсию только одного случайно выбранного бита хромосомы.
Схема функционирования
Теперь, зная как интерпретировать значения генов, перейдем к описанию функционирования генетического алгоритма. Рассмотрим схему функционирования генетического алгоритма в его классическом варианте:
- Инициировать начальный момент времени t=0. Случайным образом сформировать начальную популяцию, состоящую из k особей B_0={A_1,A_2,…,A_k}
- Вычислить приспособленность каждой особи F_{A_i}=fit(A_i), i=1…k и популяции в целом F_t=fit(B_t) (также иногда называемую термином фитнес). Значение этой функции определяет насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи.
- Выбрать особь A_c из популяции A_c=Get(B_t).
- С определенной вероятностью (вероятностью кроссовера P_c) выбрать вторую особь из популяции A_{c_1}=Get(B_t) и произвести оператор кроссовера A_c=crossing(A_c,A_{c_1}).

- С определенной вероятностью (вероятностью мутации P_m) выполнить оператор мутации A_c=mutation(A_c).
- С определенной вероятностью (вероятностью инверсии P_i) выполнить оператор инверсии A_c=inversion(A_c).
- Поместить полученную хромосому в новую популяцию insert(B_{t+1},A_c).
- Выполнить операции, начиная с пункта 3, k раз.
- Увеличить номер текущей эпохи t=t+1.
- Если выполнилось условие останова, то завершить работу, иначе переход на шаг 2.
Теперь рассмотрим подробнее отдельные этапы алгоритма.
Наибольшую роль в успешном функционировании алгоритма играет этап отбора родительских хромосом на шагах 3 и 4. При этом возможны различные варианты. Наиболее часто используется метод отбора, называемый рулеткой. При использовании такого метода вероятность выбора хромосомы определяется ее приспособленностью, то есть P_{Get{A_i}}=Fit(A_i)/Fit(B_t). Использование этого метода приводит к тому, что вероятность передачи признаков более приспособленными особями потомкам возрастает.
Другой часто используемый метод — турнирный отбор. Он заключается в том, что случайно выбирается несколько особей из популяции (обычно 2) и победителем выбирается особь с наибольшей приспособленностью.
Кроме того, в некоторых реализациях алгоритма применяется так называемая стратегия элитизма, которая заключается в том, что особи с наибольшей приспособленностью гарантировано переходят в новую популяцию. Использование элитизма обычно позволяет ускорить сходимость генетического алгоритма. Недостаток использования стратегии элитизма в том, что повышается вероятность попадания алгоритма в локальный минимум.
Другой важный момент – определение критериев останова. Обычно в качестве них применяются или ограничение на максимальное число эпох функционирования алгоритма, или определение его сходимости, обычно путем сравнивания приспособленности популяции на нескольких эпохах и остановки при стабилизации этого параметра.
Другие материалы по теме:
Loginom Community Edition — аналитика, доступная каждому
Новые возможности Loginom 6. 4. Вебинар
4. Вебинар
«Понимание индекса эволюции в фармацевтическом маркетинге: показатель эффективности»
Индекс эволюции в фармацевтическом маркетинге — это показатель, используемый для измерения и оценки прогресса лекарственного средства или терапевтического продукта на рынке.
Он учитывает различные факторы, такие как доля рынка, конкуренция, ценообразование и результаты лечения пациентов. Индекс эволюции можно использовать для отслеживания производительности продукта с течением времени и принятия обоснованных решений в отношении стратегии продукта и инвестиций.
Индекс эволюции является важным инструментом для фармацевтических компаний. Отслеживая индекс эволюции, компании могут определить ключевые тенденции и области для улучшения, а также внести коррективы в свои стратегии маркетинга и продаж, чтобы максимально использовать потенциал своей продукции.
Измерение индекса эволюции в фармацевтическом маркетинге представляет собой сложный процесс, включающий сбор, анализ и синтез данных из различных источников.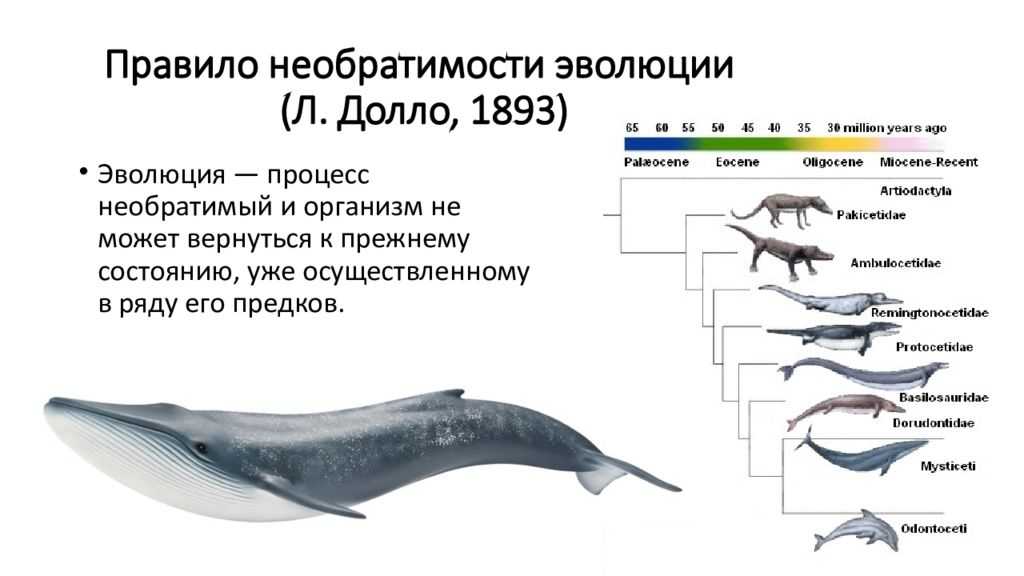
Конкретные методы, используемые для расчета индекса эволюции, могут различаться в зависимости от компании или организации, но обычно включают следующие этапы:
1 Сбор данных: Первым шагом является сбор данных о различных аспектах продукта, таких как доля рынка, результаты лечения пациентов, цены и конкуренция, среди прочего. Эти данные могут поступать из внутренних источников, таких как отчеты о продажах и маркетинге, или из внешних источников, таких как отчеты об исследованиях рынка или общедоступные данные.
2 Анализ данных: Собранные данные затем анализируются для определения эффективности продукта на рынке. Это может включать расчет доли рынка, оценку результатов лечения пациентов и сравнение цен с ценами конкурентов.
3 Синтез данных: Проанализированные данные затем синтезируются для создания комплексного представления о производительности продукта на рынке. Это может включать объединение данных в единый индекс, например оценку или рейтинг, который можно использовать для сравнения продукта с другими на рынке.
4 Расчет индекса эволюции: Последним шагом является расчет индекса эволюции, который включает в себя анализ синтезированных данных и их сравнение с предыдущими периодами времени для определения общей тенденции производительности продукта на рынке.
Важно отметить, что индекс эволюции — это постоянно развивающийся показатель, который следует регулярно обновлять, чтобы отражать изменения на рынке и в продукте. Это позволяет компаниям отслеживать эффективность своих продуктов с течением времени и принимать обоснованные решения о стратегии продукта и инвестициях.
Формула индекса эволюции в фармацевтическом маркетинге не является стандартной и может варьироваться в зависимости от компании или организации.
Конкретный расчет индекса эволюции часто является частной собственностью и может включать различные факторы и весовые коэффициенты в зависимости от целей и задач компании.
Однако, как правило, индекс эволюции можно рассчитать как совокупный балл или рейтинг, основанный на ряде факторов, таких как доля рынка, результаты лечения пациентов, ценообразование, конкуренция и нормативно-правовая среда, среди прочих. Данные об этих факторах могут быть собраны и проанализированы, чтобы создать всестороннее представление о производительности продукта на рынке.
Данные об этих факторах могут быть собраны и проанализированы, чтобы создать всестороннее представление о производительности продукта на рынке.
Например, индекс эволюции продукта можно рассчитать следующим образом:
Индекс эволюции = (Доля рынка * 0,4) + (Результаты лечения * 0,3) + (Цена * 0,2) + (Конкуренция * 0,1)
В этом примере доля рынка имеет вес 40 %, результаты лечения пациентов — 30 %, ценообразование — 20 % и конкуренция — 10 %. Веса для каждого фактора могут быть скорректированы в зависимости от важности каждого фактора для конкретного продукта и рынка.
Для фармацевта интерпретация индекса эволюции продукта является важной частью оценки его эффективности на рынке и принятия обоснованных решений в отношении стратегии продукта и инвестиций.
Интерпретация индекса эволюции должна учитывать как общий балл, так и отдельные компоненты, составляющие индекс.
Вот несколько ключевых шагов для интерпретации индекса развития:
1 Определите общий балл
2 Оцените отдельные компоненты
3 Сравните с конкурентами
4 Определите области для улучшения:
Важно регулярно обновлять индекс эволюции, отражающий изменения на рынке и в продукте.
Индекс эволюции можно использовать в качестве индикатора роста на фармацевтическом рынке. Отслеживая производительность продукта с течением времени, индекс эволюции может предоставить ценную информацию о продвижении продукта на рынке и его потенциале для будущего роста.
Более высокий балл индекса эволюции обычно указывает на то, что продукт хорошо работает на рынке и имеет большой потенциал роста, в то время как более низкий балл может указывать на области для улучшения или снижение потенциала роста. Однако важно помнить, что индекс эволюции — это лишь один из многих факторов, которые могут влиять на рост фармацевтического рынка.
В заключение следует отметить, что индекс эволюции может быть полезным инструментом для фармацевтических маркетологов, позволяющим отслеживать продвижение продукта на рынке и оценивать его потенциал роста. Регулярно отслеживая и интерпретируя индекс эволюции, маркетологи фармацевтических компаний могут принимать обоснованные решения о стратегии продукта и инвестициях, чтобы максимизировать возможности роста.
Регулярно ли вы оцениваете индекс эволюции вашей продукции для принятия взвешенных решений?
#PharmaceuticalMarketing #EvolutionIndex #GrowthPotential #Pharma #MarketingInsights #PerformanceTracking 9 0004 #ProductStrategy #DataDrivenDecisions #HealthcareMarketing #PharmaTrends
эволюционные алгоритмы — как рассчитать изменение эволюции в процентах в наборе данных по сравнению с самим собой
Задавать вопрос
спросил
Изменено
1 год, 4 месяца назад
Просмотрено
60 раз
$\begingroup$
сценарий:
Допустим, у меня есть таблица количества покупателей, посещающих магазин в день. теперь я хочу подсчитать, сколько изменений произошло с точки зрения количества посетителей за последние 30 дней, и получить одно значение, которое говорит мне о скорости изменения (в процентах). но я не хочу сравнивать изменения текущего месяца со значениями предыдущего месяца (месяцев), вместо этого я хочу сравнить текущий месяц сам с собой! У меня есть несколько наивных решений, но я не специалист по данным и не уверен, что это решение принесет мне хоть какую-то пользу!
теперь я хочу подсчитать, сколько изменений произошло с точки зрения количества посетителей за последние 30 дней, и получить одно значение, которое говорит мне о скорости изменения (в процентах). но я не хочу сравнивать изменения текущего месяца со значениями предыдущего месяца (месяцев), вместо этого я хочу сравнить текущий месяц сам с собой! У меня есть несколько наивных решений, но я не специалист по данным и не уверен, что это решение принесет мне хоть какую-то пользу!
мой первый вопрос : это вообще осмысленный вопрос (для сравнения набора данных с самим собой)?
мой второй вопрос : если да, то как бы вы подошли к решению?
решение первое : одно решение, о котором я подумал, состояло в том, чтобы сравнить значение первого дня со значением последнего дня, но тогда это казалось немного глупым, потому что значения могли колебаться случайным образом между ними, и результат не представлял бы колебания.
решение два : другое решение, которое я мог придумать, состояло в том, чтобы сравнить значение каждого дня (в пределах месяца) со значением предыдущего дня, а затем вычислить коэффициент изменения и, наконец, суммировать все отношения и получить одно значение!
примечание : я хотел бы получить как положительный, так и отрицательный процент в зависимости от коэффициента изменения
- набор данных
- эволюционные алгоритмы
$\endgroup$
$\begingroup$
Некоторые предложения:
- Ваши идеи в решениях были простыми, но надежными.
 Например, колебания второй идеи можно сгладить с помощью простой скользящей средней, и тогда применение вашей идеи будет иметь смысл.
Например, колебания второй идеи можно сгладить с помощью простой скользящей средней, и тогда применение вашей идеи будет иметь смысл. - Другая идея состоит в том, чтобы установить значение первого дня в качестве порога и вычислить общее отрицательное значение (снижение порогового значения) и положительное значение (повышение порогового значения) за месяц. Скажем, в постоянном месяце (месяце, в котором все 30 дней имеют одинаковые значения) процент изменения равен 0%. Это означает, что сумма надпороговых и подпороговых значений может дать вам оценку изменения в процентах в соответствии с первым днем. Пример
[5, 10, 50, 100, 5, 1] посещений за 6 дней. мы устанавливаем значение первого дня ($5$) в качестве порога. Тогда у вас будет[0%, 100%, 900%, 1900%, 0%, -400%]— это подъемы и падения (почему?!), и вы можете использовать любой числовой расчет, чтобы получить окончательное число, например. 2900% повышения и 400% падения, которые могут быть 2500% повышения в конце.
- Поэкспериментировав с приведенной выше идеей, можно сделать это разными способами. Вместо того, чтобы сравнивать каждый день с первым днем, как вы также упомянули, сравните его только с предыдущим днем и определите окончательную скорость изменения. Или рассмотрите штраф за негативные изменения, например. если в одном случае значения строго возрастают и окончательное изменение составляет +3000%, а в другом случае значения колеблются, но, наконец, изменение снова составляет 3000%, вы можете учитывать вес для второго, чтобы разница между ними сохранялась.
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.
