Занятия логоритмикой: Логоритмика для детей 2, 3, 4, 5, 6 лет: подходы и упражнения
Логоритмические занятия в структуре коррекционно-развивающей работы с детьми с общим недоразвитием речи в условиях ДОО
Чистая, правильная речь – одно из важнейших условий нормального психического развития человека. При помощи речи, общения ребенок легко и незаметно для себя входит в окружающий его мир, узнает много нового, интересного, может выразить свои желания, мысли, требования. К сожалению, в наши дни увеличивается количество детей с речевыми нарушениями.
Устранять нарушения речи необходимо в дошкольном возрасте, так как именно в это время нервно-психический статус детей обладает наибольшей пластичностью. Если в сензитивный период не решить эту проблему – нарушатся условия для дальнейшего полноценного развития ребёнка (Л.В. Выготский, Е.И. Винарская, В.И. Лубовский, Е.М. Мастюкова, Н.С. Жукова, Т.Б. Филичева).
В МКДОУ детский сад № 274 с 2017-2018 учебного года открыты группы комбинированной направленности, в которые зачислены дети 5-тилетнего возраста с ограниченными возможностями здоровья со следующими речевыми нарушениями: общее недоразвитие речи, II уровня речевого развития – 7,5 %, III уровня речевого развития – 81,5 % и с фонетико-фонематическим недоразвитием речи – 11%.
Общее недоразвитие речи (ОНР) рассматривается как системное нарушение речевой деятельности, сложное речевое расстройство, при которых у детей нарушено формирование всех компонентов речевой системы, касающихся и звуковой, и смысловой сторон, при нормальном слухе и сохранном интеллекте (Левина Р. Е., Филичева Т. Б., Чиркина Г. В.).
Неполноценное речевое развитие накладывает отпечаток и на формирование неречевых процессов: наблюдается недостаточная устойчивость внимания, ограничены возможности его распределения; при относительно сохранной смысловой памяти снижена вербальная память, страдает продуктивность запоминания. Имея в целом полноценные предпосылки для овладения мыслительными операциями, доступными их возрасту, дети отстают в развитии словесно-логического мышления, с трудом овладевают анализом и синтезом, сравнением и обобщением.
Общее недоразвитие речи сказывается и в отставании в развитии двигательной сферы: отмечаются плохая координация, снижение скорости и ловкости общих движений, а также недостаточная координация пальцев, кистей рук, недоразвитие мелкой моторики.
Большинство детей с ОНР не способны к длительной игровой деятельности, они не умеют ограничивать свои желания, отличаются упрямством и негативизмом.
Коррекционно-логопедическое воздействие на ребенка в процессе его всестороннего воспитания и обучения в ДОО должно быть целостным, интегрально–личностным, должно способствовать дальнейшей школьной исоциальной адаптации, готовить ребенка к полноценному и достойному участию в жизни общества.
Для эффективной реализации системы коррекционно-развивающей работы в нашей дошкольной образовательной организации, наряду с традиционными методами работы в исправлении речевых нарушений, учителем-логопедом и музыкальным руководителем проводятся логоритмические занятия (логоритмика), основанные на синтезе слова, движения и музыки.
Целью логоритмических занятий является профилактика и преодоление речевых расстройств путем развития, воспитания и коррекции двигательной сферы в сочетании со словом и музыкой.
Использование средств логоритмики в работе по коррекции нарушений речи позволяет решать широкий круг коррекционных и воспитательных задач.
В процессе занятий логоритмикой с детьми дошкольного возраста выделяют два основных направления работы:
1. Развитие неречевых процессов: совершенствование общей и мелкой моторики, координации движений, ориентации в пространстве; регуляции мышечного тонуса; развития музыкального темпа и ритма, певческих способностей; активация всех видов внимания и памяти.
2. Развитие речевых процессов и коррекция имеющихся у детей нарушений речи включают: развитие дыхания, голоса; выработку умеренного темпа речи и ее интонационной выразительности; развитие артикуляционной и мимической моторики; координацию речи с движением; воспитание правильного звукопроизношения и формирование фонематического слуха.
Концепция организации логоритмических занятий с детьми старшего дошкольного возраста основывается на традиционных принципах педагогики и дидактики (принцип наглядности, принцип всестороннего воздействия, принцип учёта симптоматики, принцип этапности).
При проведении логоритмических занятий с воспитанниками с ограниченными возможностями здоровья логопед и музыкальный руководитель предъявляют единые требования. Занятия логоритмикой проводятся 1 раз в неделю в музыкальном зале. Каждое занятие проводится по лексической теме, в соответствии с тематическим планированием коррекционно-логопедической работы, в игровой форме, от 25 до 30 минут в зависимости от возраста детей. Занятия состоят из трёх частей: подготовительной, основной и заключительной.
Подготовительная часть продолжается от 3 до 7 минут. Данное время необходимо для подготовки организма ребёнка к моторной и речевой нагрузкам. Используются такие упражнения, как повороты и наклоны корпуса, различные виды ходьбы и бега с движениями руками, с изменением направления и темпа движения, с перестроениями. С помощью этих упражнений дети учатся ориентироваться в пространстве, в право- левостороннем направлении движения и т.д. Вводные упражнения дают установку на разнообразный темп движения и речи с помощью музыки и направлены на тренировку внимания, памяти и ориентировки, тормозных реакций.
Основная часть длится 10-15 минут и может содержать следующие виды деятельности:
Ходьба и маршировка в различных направлениях.
Упражнения на развитие дыхания, голоса, артикуляции.
Упражнения, регулирующие мышечный тонус.
Упражнения, активизирующие внимание.
Фонопедические упражнения.
Упражнения на развитие координации движения.
Упражнения на координацию речи с движением;
Упражнения, на координацию пения с движением;
Речевые упражнения без музыкального сопровождения;
Упражнения, формирующие чувства ритма;
Упражнения, формирующие чувство музыкального темпа;
Упражнения на развитие мелкой моторики;
Ритмические упражнения;
Упражнения для развития творческой инициативы.
Чистоговорки.
Пение.
Слушание музыки для снятия эмоционального напряжения.
Игра на музыкальных инструментах.
Игры (статические, малоподвижные, подвижные).
Коммуникативные игры.
Мимические этюды.
Хороводы.
Заключительная часть занимает от 2 до 7 минут и состоит из упражнений на восстановление дыхания, снятия мышечного и эмоционального напряжения, спокойной ходьбы, релаксационных упражнений.
Эффективность коррекционно-развивающей работы с детьми с ограниченными возможностями здоровья определяется четкой организацией их пребывания в детском саду, правильном распределении нагрузки в течение дня и преемственностью в работе логопеда и других специалистов ДОО. Занятия логоритмикой – вспомогательное средство для эффективной совместной работы логопеда и музыкального руководителя по развитию и коррекции речи воспитанников комбинированных групп с речевыми нарушениями.
Список литературы
1. Буренина А.И. Ритмическая пластика для дошкольников – СПб.
: 1994.
2. Волкова Г.А. Логопедическая ритмика — М.: ВЛАДОС, 2003.
3. Воронова Е.А. Логоритмика в речевых группах ДОУ для детей 5 – 7 лет Методическое пособие – М.: ТЦ Сфера, 2006.
4. Картушина М.Ю. Логоритмические занятия в детском саду – М.: ТЦ Сфера, 2005.
5. Лопухина И.С. Логопедия. Речь, ритм, движение. – СПб.: Дельта, 2001.
6. Макарова Н.Ш. Коррекция неречевых и речевых нарушений у детей дошкольного возраста на основе логопедической ритмики — СПб.: ДЕТСТВО-ПРЕСС, 2009.
7. Мухина А.Я. Речедвигательная ритмика – М.: Астрель, 2009.
8. Новиковская О.А. Логоритмика – СПб.: Корона принт., 2005.
9. Пожиленко Е.А. Артикуляционная гимнастика – СПб.: КАРО, 2004.
10. Федорова Г.П. Поиграем, потанцуем – СПб.: Акцидент, 1997.
конспекты занятий по логоритмике на три месяца для детей старшего дошкольного возраста с ЗПР | План-конспект занятия (старшая группа) на тему:
НОВЫЙ ГОД
Цель:
— формировать двигательные умения и навыки;
-развивать ловкость, силу, координацию движений;
-развивать музыкальные способности детей (слуховое восприятие, ритм, темп, тембр)
-стимулировать и обогащать творческие проявления детей в игре.
Ход занятия
- Динамическое упражнение «Мы на лыжах в лес идем»
Мы на лыжах в лес идем,
Мы взбираемся на холм.
Палки нам идти помогут,
Будет нам легка дорога.
(Дети машут руками, словно работают лыжными палками)
Вдруг поднялся сильный ветер,
Он деревья крутит, вертит
И среди ветвей шумит.
Снег летит, летит, летит.
(Вращение туловищем вправо и влево)
По дорожке, по дорожке
Скачем мы на правой ножке
(Подскоки на правой ноге)
И по этой же дорожке
Скачем мы на левой ножке.
(Подскоки на левой ноге)
По тропинке побежим,
До лужайки добежим.
(Бег на месте)
На лужайке, на лужайке
Мы попрыгаем, как зайки.
(Прыжки на месте на обеих ногах)
Вверх потянулись,
Всем улыбнулись
Вот мы и пришли на лесную полянку. Вокруг снег лежит да мороз трещит. Замерзли?
- Комплекс дыхательных упражнений «Погреемся» (авторская разработка)
Сильный мороз,
Заморозил наш нос.
Носик погреем,
Подышим скорее.
(Вдох через нос, шумный выдох в ладошку, которой прикрыто лицо)
Отогрели нос,
А подбородок замерз.
(Глубокий вдох через нос, втянуть нижнюю губу под верхнюю, длительно бесшумно подуть вниз на подбородок)
Ладошки погреем –
Дышим веселее!
(Выдох на ладошки, произнося слог «фа»)
Мерзнут ножки наши?
Весело попляшем!
(Дети выполняют приседания, произнося слог «ух»)
Педагог: Налетел вдруг ветерок –
Шаловливый паренек.
Снежинки в небо он поднял
И с ними вальс затанцевал.
- Активное слушание контрастной музыки «Ветерок и снежинки»
Во время звучания стремительной музыки «Зимы» А. Вивальди мальчики-ветерки легко бегают врассыпную по залу с голубыми султанчиками в руках и произносят «ш-ш-ш». При смене музыкального материала на нежный «Вальс» Е. Доги мальчики «замирают», а девочки-снежинки импровизируют танцевальные движения с легкими белыми шарфами.
Педагог: Все летали, все кружились,
И на землю опустились.
Мы присядем на пенек,
Разомнем свой язычок.
- Комплекс артикуляционных упражнений «Котик Рыжик зимой»
Раз-два-три-четыре-пять
Будем с Рыжиком гулять!
Раз-два-три-четыре
Рот откроем мы пошире. широко раскрыть рот, подержать несколько секунд;
Пожевали, жевательные движения с закрытым ртом;
Постучали постучать зубами;
И с котенком побежали. движение языком вперед-назад;
Кот снежинки ртом ловил, ловить ртом воображаемые снежинки;
Влево, вправо он ходил. движение языком вправо-влево;
Скучно Рыжику, ребятки,
Поиграем с ним мы в прятки. то втягивать губы внутрь рта, то высовывать узкий напряженный язык;
Рыжик прятаться устал,
Рыжик «Ух!» сердитым стал. выгибание вверх и продвижение вперед спинки языка, кончик языка при этом прижимается к нижним зубам;
Мы погладим котика,
Все покажем ротиком.
упражнение «Расчесочка»
- Речевая игра со звучащими жестами «Ты, мороз»
Ты, мороз, мороз, мороз, идут в круг, грозят пальцем;
Не показывай свой нос! показывают двумя руками «нос»;
Уходи скорей домой, ладошками «отгоняют»;
Стужу уноси с собой. кружатся вокруг себя, притопывая;
А мы саночки возьмем бегут по кругу друг за другом, потирая
И на улицу пойдем. ладошками;
Сядем в саночки-самокаточки!
С горки останавливаются, поднимают вверх руки;
Упали! резко приседают, опуская руки;
От Мороза убежали! разбегаются, Мороз догоняет
Педагог: Мороз приходил,
Нам сказку подарил.
Ее не только мы расскажем,
Мы ручками ее покажем.
- Пальчиковая сказка «Рукавичка»
Из-за леса, из-за гор
Топал дедушка Егор.
шлепают ладошками по коленям;
Очень он домой спешил –
Рукавичку обронил. показывают обратную сторону ладони с вытянутым вверх большим пальцем – жест «Рукавичка»;
Мышка по полю бежала, «бегают» пальчиками одной руки по другой руке;
Рукавичку увидала. жест «Рукавичка»;
Кто, кто здесь живет? стучат правым кулачком по левой ладошке;
Мышку здесь никто не ждет? грозят пальцем;
Стала жить-поживать,
Звонко песни распевать. хлопки;
Зайка по полю бежал, жест «Зайчик»;
Рукавичку увидал. жест «Рукавичка»;
Кто, кто здесь живет? стучат правым кулачком по левой ладошке;
Звонко песенку поет? хлопки;
Мышка Зайку пригласила, зовут правой рукой;
Сладким чаем напоила. вытягивают вперед руки, ладошки «чашечкой»;
Зайка прыг, зайка скок,
Вкусных пирогов напек.
«пекут» пирожки;
Как по полю шла лисичка, мягкие движения кистями рук;
Увидала рукавичку. жест «Рукавичка»;
Кто, кто здесь живет? стучат правым кулачком по левой ладошке;
Звонко песенку поет? хлопки;
И лисичку пригласили, мягкие движения кистями рук;
Пирожками угостили. «пекут» пирожки;
Стала жить там поживать,
Пол метелкой подметать. движения руками влево-вправо;
Мишка по полю гулял, стучат кулачками по коленям;
Рукавичку увидал жест «Рукавичка»;
Кто, кто здесь живет? стучат правым кулачком по левой ладошке;
Звонко песенку поет? хлопки;
Звери испугались, сжать пальцы рук в замок;
В страхе разбежались. развести руки в стороны.
Восп.: Грустно стало Мишке. Он так хотел пирожки попробовать! Ребята, а с какой начинкой вы любите пирожки?
- Подвижная игра «Гора – дерево – кочка»
Дети бегают врассыпную по залу под музыку, помахивая руками, как крыльями. Когда музыка обрывается, логопед говорит: «Кочка!» — дети приседают; «Дерево!» — замирают, подняв руки вверх; «Гора!» — встают на колени и поднимают соединенные руки вверх.
- «Танец снежинок» под песню «Снежная сказка» В. Лемита.
- Песня по желанию детей про новый год.
- Релаксация.
Логоритмика ♫ занятия для детей
Развитие речи логоритмикой
Логоритмика или логопедическая ритмика – это коррекционное занятие для запуска и развития речи у малышей от 2 лет и старше. В основе метода – соединение музыки, движения и речи.
Цели и задачи занятий:
- преодолеть задержку речевого развития;
- улучшить качество речи: произношение, темп, ритм;
- улучшить двигательные и моторные навыки;
- совершенствовать фонематический слух;
- развивать навыки коммуникации с другими детьми, социальные навыки.
Также занятия развивают память, внимание, восприятие на слух, улучшают эмоциональное состояние ребенка.
Использование логоритмики очень широкое: при заикании, ЗРР, ОНР, алалии (для неговорящих детей), ринолалии, дизартрии, проблемах с артикуляцией, произнесением и темпом речи, а также для коррекции речевых нарушений в составе комплексной реабилитации детей с ДЦП, ЗПР и др. ОВЗ.
Методы и элементы логоритмики для малышей
На занятиях используются:
- Игровой метод – упражнения подаются в игровой форме, чтобы ребенку было весело и увлекательно. Все игры – музыкально-ритмические.
- Подражание – ребенок повторяет упражнения за педагогом.
- Звукоподражание
- Пальчиковая гимнастика – стихи и песни сопровождаются упражнениями для рук, ведь развитие мелкой моторики и речи тесно связаны.
Основной элемент логоритмических занятий – музыка. Музыка для логоритмики подбирается с учетом возраста детей, их интересов. Используются отрывки из мультфильмов, развивающие логопедические детские песни, звуки природы и др. Более того, дети сами участвуют в создании звуков с помощью музыкальных инструментов. Логоритмика под музыку проходит весело и познавательно.
Движение – еще один важный элемент занятия. Ребята под музыку повторяют движения за педагогом, отбивают ритм на музыкальных инструментах. Так тренируется моторика, чувство ритма.
Пение – еще одна составляющая занятия. Поем гласные звуки «а», «о», «у», «и», «э», слоги, а также специальные песенки, адаптированные под упражнения.
Эти элементы хорошо видно на видео.
Подходят ли упражнения на логоритмике для детей с особенностями развития
Детская логоритмика в нашем центре полностью адаптирована под возможности и потребности особых малышей.
Специалисты подстраивают программу под каждого конкретного ребенка и помогают выполнять упражнения правильно.
Для малышей, которые сами не могут удерживать правильное положение тела, есть специальные удобные стульчики и ассистирующий педагог.
Для какого возраста подойдет
Наиболее эффективна логоритмика для дошкольников при активном освоении речи. Обычно этот период попадает на возраст 2-4 года. Но, в зависимости от тяжести нарушений работы нервной системы, развитие речи может существенно запаздывать. Поэтому логоритмика может быть актуальной и в 5, 6, 7 лет и старше.
Занятия по логоритмике в центре «Наш Всесвіт» Харьков
Логоритмика в нашем реабилитационном центре – групповое занятие. Группы занимаются на постоянной основе, начать можно с любого занятия. С детьми работает опытный коррекционный педагог. Мы используем методики Е. Железновой, М.
Картушиной, Т. Овчинниковой, В. Смердовой и др.
Наша музыкальная логоритмика очень нравится детям.
Занятия по логоритмике для детей проходят в хорошо оборудованном комфортном помещении. Мы расположены на Алексеевке возле метро Победа.
| Цена | 250 грн |
| Длительность | 45 мин |
Логопедическая ритмика для детей для лучшего эффекта отлично совмещается с Томатис-терапией и занятиями с логопедом.
Но логоритмика это не только совместная работа специалистов и ребенка, но и его семьи, требующая регулярности. Наш педагог с радостью покажет родителям какие упражнения нужно делать дома, чтобы закрепить результат. Если вы сомневаетесь, подойдут ли вашему ребенку эти занятия – запишитесь на консультацию для родителей, вы сможете задать все интересующие вас вопросы специалисту.
Отзывы
Чтобы почитать отзывы о специалистах и работе центра – посетите наши страницы в Facebook и Instagram
алгоритмов | Coursera
Skills you will gain
- Algorithms
- Dynamic Programming
- Greedy Algorithm
- Divide And Conquer Algorithms
- Randomized Algorithm
- Sorting Algorithm
- Graphs
- Data Structure
- Hash Table
- Spanning Tree
- Np-Completeness
Об этой специализации
57 487 недавних просмотров
Алгоритмы являются сердцем информатики, и этот предмет имеет бесчисленное количество практических применений, а также интеллектуальную глубину.
Эта специализация представляет собой введение в алгоритмы для учащихся, имеющих хотя бы небольшой опыт программирования. Специализация является строгой, но делает упор на общую картину и концептуальное понимание, а не на низкоуровневую реализацию и математические детали. После завершения этой специализации вы сможете успешно пройти технические собеседования и свободно говорить об алгоритмах с другими программистами и учеными-компьютерщиками.
О преподавателе: Тим Рафгарден является профессором факультета компьютерных наук Стэнфордского университета с 2004 года. Он преподавал и много публиковался на тему алгоритмов и их приложений.
Учащиеся будут практиковать и осваивать основы алгоритмов с помощью нескольких типов оценок. Каждую неделю проводится викторина с несколькими вариантами ответов, чтобы проверить ваше понимание наиболее важных понятий. Есть также еженедельные задания по программированию, где вы реализуете один из алгоритмов, описанных в лекции, на выбранном вами языке программирования.
Каждый курс завершается выпускным экзаменом с несколькими вариантами ответов.
Общий сертификат
Общий сертификат
Получите сертификат по завершении
100 % онлайн-курсы
100 % онлайн-курсы
Начните сразу и учитесь по собственному графику.
Гибкий график
Гибкий график
Устанавливайте и соблюдайте гибкие сроки.
Средний уровень
Средний уровень
Требуется некоторый соответствующий опыт.
Часов до завершения
Приблизительно 4 месяца до завершения
Рекомендуемый темп 4 часа в неделю
Доступные языки
Английский
Субтитры: английский, арабский, французский, португальский (европейский), итальянский, вьетнамский, немецкий, русский, испанский
Совместно используемый сертификат
Совместно используемый сертификат
Получите сертификат по завершении
100 % онлайн-курсы
100 % онлайн-курсы
Начните немедленно и учитесь по собственному графику.
Гибкий график
Гибкий график
Устанавливайте и соблюдайте гибкие сроки.
Средний уровень
Средний уровень
Требуется некоторый соответствующий опыт.
Часов на выполнение
Приблизительно 4 месяца на выполнение
Предлагаемый темп 4 часа в неделю
Доступные языки
Английский
Субтитры: английский, арабский, французский, португальский (европейский), итальянский, вьетнамский, немецкий, русский, испанский
Как работает специализация курсы, которые помогут вам овладеть навыком. Для начала зарегистрируйтесь на специализацию напрямую или просмотрите ее курсы и выберите тот, с которого вы хотите начать. Когда вы подписываетесь на курс, являющийся частью специализации, вы автоматически подписываетесь на полную специализацию. Можно пройти только один курс — вы можете приостановить обучение или отменить подписку в любое время. Посетите панель учащегося, чтобы отслеживать зачисление на курс и свой прогресс.
Практический проект
Каждая специализация включает практический проект. Вам нужно будет успешно завершить проект(ы), чтобы завершить специализацию и получить сертификат.
Если специализация включает в себя отдельный курс для практического проекта, вам нужно будет пройти все остальные курсы, прежде чем вы сможете приступить к нему.
Получите сертификат
По окончании каждого курса и выполнения практического проекта вы получите сертификат, которым сможете поделиться с потенциальными работодателями и членами своей профессиональной сети.
Инструктор
Тим Гроугарден
Профессор
Компьютерная наука
320,124 Учащиеся
6 . Стэнфордский университет или Стэнфорд — американский частный исследовательский университет, расположенный в Стэнфорде, Калифорния, на территории кампуса площадью 8 180 акров (3310 га) недалеко от Пало-Альто, Калифорния, США.
Часто задаваемые вопросы
Какова политика возврата?
Могу ли я просто записаться на один курс?
Доступна ли финансовая помощь?
Могу ли я пройти курс бесплатно?
Этот курс действительно на 100% онлайн? Нужно ли мне лично посещать какие-либо занятия?
Сколько времени занимает прохождение специализации?
Какие базовые знания необходимы?
Нужно ли проходить курсы в определенном порядке?
Получу ли я университетский кредит за завершение специализации?
Что я смогу делать после завершения специализации?
Есть вопросы? Посетите Справочный центр для учащихся.
Алгебра — Логарифмические функции
Онлайн-заметки Пола
Дом
/
Алгебра
/
Экспоненциальные и логарифмические функции
/ Логарифмические функции
Показать мобильное уведомление
Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.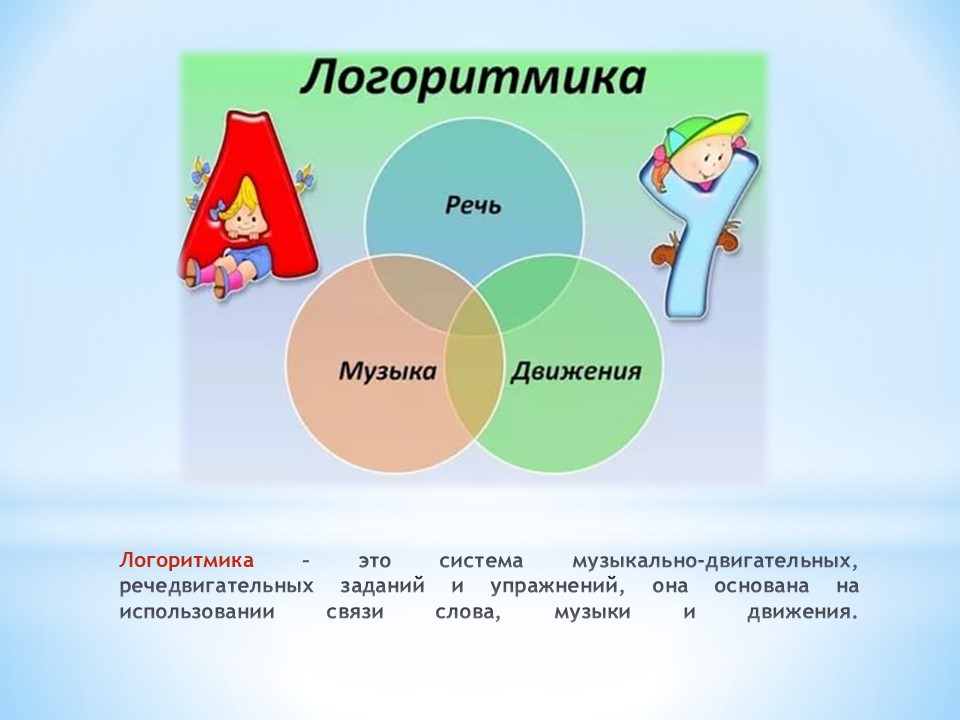
Раздел 6-2: Логарифмические функции
В этом разделе нам нужно перейти к логарифмическим функциям. Это может быть сложной функцией для построения графика сразу. Будут некоторые другие обозначения, к которым вы не привыкли, и некоторые свойства могут быть не такими интуитивными. Однако не отчаивайтесь. Как только вы разберетесь с ними, вы обнаружите, что они на самом деле не так уж плохи, и обычно требуется немного поработать с ними, чтобы понять их. 9y} = x\) называется экспоненциальной формой .
Обратите внимание, что требование \(x > 0\) на самом деле является результатом того факта, что мы также требуем \(b > 0\). Если вы думаете об этом, это будет иметь смысл. Мы возводим положительное число в степень, поэтому результат не может быть ничем иным, как другим положительным числом. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.
Теперь давайте обратимся к используемым здесь обозначениям, так как обычно это самое большое препятствие, которое ученики должны преодолеть, прежде чем начать понимать логарифмы. Во-первых, «логарифмическая» часть функции — это просто три буквы, которые используются для обозначения того факта, что мы имеем дело с логарифмом. Они не являются переменными и не означают умножения. Они здесь только для того, чтобы сказать нам, что мы имеем дело с логарифмом. 9x}\) в такой форме, но это не так. Просто похоже, что это может быть то, что происходит.
Важно соблюдать прямолинейность записи логарифмов, иначе вам будет очень сложно их понять и работать с ними.
Теперь давайте кратко рассмотрим, как мы вычисляем логарифмы.
Пример 1 Оцените каждый из следующих логарифмов.
- \({\log _4}16\)
- \({\log _2}16\)
- \({\log _6}216\)
- \(\displaystyle {\log _5}\frac{1}{{125}}\)
- \({\log _{\frac{1}{3}}}81\)
- \({\log _{\frac{3}{2}}}\displaystyle \frac{{27}}{8}\)
Показать все решения Скрыть все решения
Показать обсуждение
Реальность такова, что прямое вычисление логарифмов может быть очень сложным процессом, даже для тех, кто действительно в них разбирается.
Обычно гораздо проще сначала преобразовать логарифмическую форму в экспоненциальную. В такой форме мы обычно можем получить ответ довольно быстро. 94}\), и т. д. , пока не получите 16. В этом случае нам нужен показатель степени 4. Следовательно, значение этого логарифма равно
.
\[{\log _2}16 = 4\]
Перед тем, как перейти к следующей части, обратите внимание, что основа для них является очень важной частью обозначений. Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.
c \({\log _6}216\) Показать решение
93}}} = \frac{{27}}{8}\]
Надеюсь, теперь у вас есть представление о том, как вычислять логарифмы, и вы начинаете разбираться в обозначениях. Есть еще несколько оценок, которые мы хотим сделать, однако нам нужно ввести некоторые специальные логарифмы, которые встречаются на очень регулярной основе.
Это десятичный логарифм и натуральный логарифм . Вот определения и обозначения, которые мы будем использовать для этих двух логарифмов.
\[\ begin{align*}& {\mbox{десятичный логарифм:}}\hspace{0,25 дюйма}\log x = {\log _ {10}}x\\ & {\mbox{натуральный логарифм:}}\ hspace {0,25 дюйма} \ ln x = {\ log _ {\ bf {e}}} x \ end {align *} \]
Итак, десятичный логарифм — это просто логарифм по основанию 10, за исключением того, что мы опустили часть обозначения «по основанию 10». Точно так же натуральный логарифм — это просто логарифмическая база \(\bf{e}\) с другим обозначением, где \(\bf{e}\) — то же число, которое мы видели в предыдущем разделе и определяется как \({\bf{e}} = 2,718281828 \ldots\).
Давайте взглянем еще на пару оценок.
Пример 2 Оцените каждый из следующих логарифмов.
- \(\лог 1000\)
- \(\log \displaystyle \frac{1}{{100}}\)
- \(\ln \displaystyle \frac{1}{{\bf{e}}}\)
- \(\ln \sqrt {\bf{e}} \)
- \({\log _{34}}34\)
- \({\log _8}1\)
Показать все решения Скрыть все решения
Показать обсуждение
Чтобы выполнить первые четыре вычисления, нам просто нужно помнить, как они обозначаются и какое основание подразумевается этими обозначениями.
Последние две оценки должны проиллюстрировать некоторые свойства всех логарифмов, которые мы в конечном итоге рассмотрим. 90} = 1\). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.
Итак, при вычислении логарифмов все, что мы действительно спрашиваем, это какой показатель степени мы положили в основание, чтобы получить число в логарифме.
Теперь, прежде чем мы перейдем к некоторым свойствам логарифмов, давайте сначала нарисуем пару быстрых графиков.
Пример 3 Нарисуйте график десятичного логарифма и натурального логарифма на одной системе координат.
Показать решение
Этот пример имеет две точки. Во-первых, он познакомит нас с графиками двух логарифмов, которые мы, скорее всего, увидим в других классах. Кроме того, это даст нам некоторую практику использования нашего калькулятора для оценки этих логарифмов, потому что реальность такова, что именно так нам нужно будет выполнять большинство этих оценок.
Вот таблица значений двух логарифмов.
| \(х\) | \(\лог х\) | \(\ln х\) |
|---|---|---|
| \(\frac{1}{2}\) | -0,3010 | -0,6931 |
| 1 | 0 | 0 |
| 2 | 0,3010 | 0,6931 |
| 3 | 0,4771 |
Нам просто нужно быть осторожными с этими свойствами и использовать их правильно.
5}} \вправо)\]
Кроме того, мы можем иметь дело с показателями степени только в том случае, если член в целом возводится в степень. Тот факт, что обе части этого термина возведены в квадрат, не имеет значения. Это должен быть весь член в квадрате, как в первом логарифме.
8}} \right)\]
Если бы 7 была 5, или 25, или 125, и т. д. . мы могли бы сделать это, но это не так. Поэтому приходится использовать формулу замены основания.
Лучшие модели смогли ответить только на математические вопросы начального или старшего школьного возраста, и они не всегда находят правильные решения.
Систему также можно использовать в качестве автоматизированного репетитора, который показывает учащимся этапы решения математических задач бакалавриата.
Исследование появилось на этой неделе в Proceedings of the National Academy of Sciences. 
Студент уловит этот контекст во время прохождения курса, но у нейронной сети нет этих фоновых знаний, если только исследователи не укажут это.
Например, были вопросы о квантовом обнаружении горизонтальных и вертикальных линий, и это породило новые вопросы о квантовом обнаружении диагональных линий. Таким образом, это не просто создание новых вопросов путем замены значений и переменных в существующих вопросах», — говорит Дрори.