Олимпиада по математике

• Когда будет проходить?

  11 октября – 14 ноября 2022 г. Выполнить задания можно в любой из этих дней, на работу даётся час.

• Как получить доступ учителю и родителю?

  Нужно зарегистрироваться на Учи.ру и затем войти в олимпиаду с помощью ваших логина и пароля. Обратите внимание: логин — адрес электронной почты, который вы указали при регистрации.

  Если у вас уже есть аккаунт на Учи.ру, регистрироваться заново не нужно, просто используйте свои логин и пароль для входа в олимпиаду.

• Как открыть доступ ученикам?

  Войдите в личный кабинет на Учи.ру и создайте электронный список класса, в котором нужно указать имя, фамилию и пол каждого ученика. Система придумает логины и пароли, распечатайте их и раздайте классу, чтобы ученики смогли принять участие в олимпиаде. Вы можете зарегистрировать неограниченное количество классов и учеников.

• Как провести олимпиаду в своей школе?

  Для этого необходим доступ к интернету и компьютер или планшет с современным браузером для каждого участника. Проверьте работоспособность техники до начала основного тура, его можно пройти только один раз.

  Мы рекомендуем провести репетицию за пару дней до начала соревнования:

  1. Посадите учеников за компьютеры.

  2. Раздайте им логины и пароли и попросите зайти на сайт UCHi.RU.

  3. Дайте им возможность потренироваться на обучающих задачах.

  Если возникнут технические проблемы, обратитесь к школьному системному администратору. Возможно, придётся обновить веб-браузер или проверить соединение с интернетом.

• В каких веб-браузерах можно пройти олимпиаду?

  Рекомендуем использовать:

  • операционные системы: Windows 10, MacOS 10, iOS 10, Android 7 и выше;

  • последние версии браузеров: Google Chrome, Mozilla Firefox, Safari, Microsoft Edge, Яндекс.Браузер.

  Мы не гарантируем работу сайта в других операционных системах и браузерах.

• Где можно будет посмотреть результаты?

  Результаты обучающих задач будут обновляться в личном кабинете каждый раз, когда ученик будет сдавать задачу.

  Результаты задач олимпиады появятся в личных кабинетах сразу после окончания олимпиады. Награды будут зависеть от количества набранных баллов.

  Напоминаем, что результаты обучающих задач никак не связаны с результатами задач олимпиады.

• Почему онлайн?

  У онлайн-олимпиад есть важные преимущества:

  • Удобно. Присоединиться можно из любой точки страны и мира, если есть компьютер и доступ в интернет.

  • Быстро. Результат будет сразу после завершения работы.

  • Интересно. Формат нравится школьникам, он ассоциируется с отдыхом и развлечениями.

• Может ли взрослый решить задания за ребёнка?

  Олимпиада создана для школьников, и мы ждем, что ученики будут решать задачи самостоятельно. Алгоритмы помогают нам определить, выполнял ребёнок задания сам или со взрослыми.

• Кто проводит олимпиаду?

  Платформа Учи. ру

По любым вопросам вы можете писать на [email protected]

Олимпиада Учи.ру по математике: ответы на задания

Содержание

• 1 Как участвовать
• 2 Как пройти задания
• 3 Задания и ответы
  • 3.1 Батарейки для робота
  • 3.2 Собери квадрат
  • 3.3 Рамка
  • 3.4 Мосты Хрума
  • 3.5 Снеговики
  • 3.6 Качели для обезьян
  • 3.7 База для корабля
  • 3.8 Голодная птица
  • 3.9 Фальшивый камень
  • 3.10 Дырокол
  • 3.11 Сколько кошек и собак
  • 3.12 Набор варенья
  • 3.13 Где клад?
• 4 Призовой фонд

С 11 октября 2022 года на образовательной платформе Учи.ру стартовала новая бесплатная олимпиада по математике. Как и ранее принять в ней участие могут ученики 1-9 классов всех образовательных учреждений. Для участия не нужны специальные знания по предмету и особая подготовка. Главное в процессе прохождения проявить внимание, смекалку и немного терпения.

Как участвовать

Участвовать в олимпиаде по математике могут школьники 1-9 классов. Для участия нужно войти в личный кабинет платформы Учи.ру с помощью логина и пароля, или кода приглашения от учителя.

Новые пользователи платформы могут зарегистрироваться самостоятельно. Важно, чтобы в этот момент рядом находился родитель и помог внести все данные без ошибок.

Как пройти задания

На решение заданий дается 1 час. Остановить задачи и взять паузу нельзя. Если вы затрудняетесь ответить на какой-то вопрос, вы можете пропустить его и вернуться к нему позже. После нажатия кнопки «завершение олимпиады» или истечения времени, на экране отобразятся результаты с количеством набранных баллов.

Задания и ответы

Правильные ответы на задания текущей олимпиады можно посмотреть в течение двух недель после её окончания на странице соревнования. Всего в разделы решений входят 10 этапов задач. Рассмотрим каждый из них.

Батарейки для робота

Суть задания состоит в том, что у робота закончилась энергия. Какой-то там крокодил Хрум собрал для робота батарейки из одинаковых кубиков. Нужно найти ту батарейку, которая войдёт в гнездо и зарядит робота, так как не все батарейки поместятся в робота, вот и придётся проверить все батарейки, и выделить только те, которые можно погрузить в робота.

Выбери все батарейки, которые можно установить в робота. Тебе видны все кубики. Нужно выделить фигуры при помощи нажатия курсором на них,, которые подходят под верный ответ. Задача для подготовительного (нулевого) и 1 класса на учи.ру, в ответе будет три фигуры, смотрите фото ниже:

Задача для 2 класса, тут уже будет пять фигур:

Задача 3 класс:

Задача 4 класс:

Собери квадрат

Суть задания в том, что надо собрать один квадрат из всех фигур. Фигуры не должны пересекаться. Внутри квадрата не должно быть пустых клеток. Нажимая курсором на фигуру, она вращается, держа левой кнопкой мышки её можно передвинуть.

Собери один квадрат из всех фигур. Фигуры не должны пересекаться. Внутри квадрата не должно быть пустых клеток. Задача для подготовительного (нулевого) класса, чтобы быстрее собрать, посчитайте, сколько квадратов должно быть в одной стороне.

Задача для 2 класса:

Задача для 3 класса, ответ:

Задача для 4 класса, ответ:

Рамка

В этом задании надо передвигать рамку так, чтобы в неё попало 5 вишенок. Найди как можно больше решений. Каждый пряник может попасть в несколько решений.

Найди как можно больше решений так, чтобы сумма чисел внутри рамки была равна 5. Рамку можно вращать, для этого слева внизу нажмите на кнопку «Повернуть рамку», а когда установили её верно, нужно нажать справа на кнопку «Сохранить решение», чтобы зафиксировать ответ. Задача для подготовительного (нулевого) класса, всего решений будет четыре, смотрите ответ ниже:

Мосты Хрума

Помоги Капитану Хруму восстановить мост, используя только 2 детали на выбор. Не забывай переворачивать детали, если понадобится. Достаточно всё просто, в реке контур моста, надо его заполнить фигурами, которые разместились по берегам, как видно из условия, не забывая поворачивать детали.

Восстанови мост, используя только 2 детали на выбор. Не забывай переворачивать детали, если понадобится. Задача для подготовительного (нулевого) класса, два действия:

Снеговики

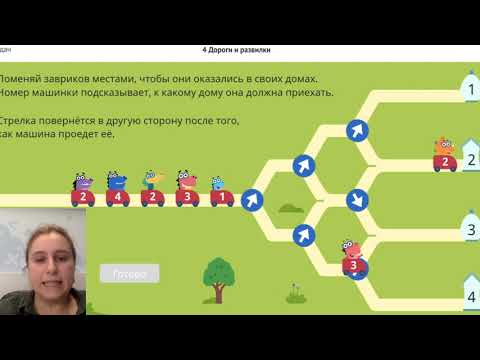
Заврики лепят снеговиков. Помоги каждому заврику докатить снежок до снеговика в шапке такого же цвета. Для этого поставь блоки с дорожками на поле.

Помоги каждому заврику докатить снежок до снеговика в шапке такого же цвета. Для этого расставь блоки с дорожками на поле. Блоки надо брать левой кнопкой мышки и перетаскивать в нужное место. Задача для подготовительного (нулевого) класса, ответ не из лёгких, ребёнок, котрый не решал такие задачи ранее может запутаться.

Качели для обезьян

В задании надо посадить обезьянку на одну из лиан так, чтобы бревно выровнялось. Чем дальше от центра бревна висит обезьянка, тем больше его наклон.

Посади всех обезьянок на лианы так, чтобы бревно висело ровно. Помни: чем дальше от центра бревна висит обезьянка, тем больше его наклон. Вариантов решений может быть несколько, вот один из них:

База для корабля

Доведи корабли до их баз. Поворачивай льдины, чтобы передвигать корабли. Чтобы это сделать, необходимо вращать льдины с кораблями, с каждым вращением которых корабль всё далее вести до базы и не забывать, чтобы цвет корабля совпадал с цветом базы.

Льдину можно повернуть, если сбоку от неё есть корабль. Задача для 1 класса:

2, 3 и далее классы будут несколько меняться базы и корабли, но смысл один и тот же, как и большое количество решений.

Голодная птица

Голодная птица открывает рот в ту сторону, где больше еды.

Меняй местами и переворачивай пледы так, чтобы птица открывала рот в сторону, где больше кусочков пирога. А это значит, что можно удерживая левую кнопку мышки поменять пледы с едой местами, а не только их поворачивать. Задача для 1 класса, по своей сути это задача на неравенство.

Задача для 2 класса, если сравнить с 1 классом, то пледы изменились, но смысл остался тот же.

Задача для 3 класса.

Задача для 4 класса.

Фальшивый камень

В коллекции 7 камней одного веса. Ещё один камень — фальшивый, он легче настоящего. Найди его с помощью весов. Сделай как можно меньше взвешиваний. Нажимай на камни или зажми кнопку мыши и потяни, чтобы выбрать нужное количество. Задача для 1, 2, 3 класса Есть одинаковые камни, по идее они должны весить одинаково, на примере я показал 4 взвешивания, за что получил оценку 7, хотя задачу можно было решить в 2 или 1 этапа и получить оценку 10. Тут так, чем больше взвешиваний, тем меньше оценка.

Каждый раз фальшивый камень меняется! Фальшивым может быть как парный, так и не парный, поэтому сначала рекомендую сразу все парные взвесить.

Дырокол

Лист сложили один раз и сделали дырку. По условию задачи надо отметить, где будут дырки, если лист развернуть.

Пример был простой, а вот задание уже посложнее, справа развёрнутый лист и надо найти все отверстия на нём, которые продырявил дырокол. Также слева находится схема, как складывали лист. Задача для 1 класса.

Задача для 2 класса.

Задача для 3 класса.

Задача для 4 класса.

Сколько кошек и собак

Сколько на каждом этаже собак и кошек? Впиши ответы цифрами. Задача для 1 и 2 класса.

• На 1 этаже 9 собак и кошек. Кошек на 5 больше, чем собак. Ответ: кошек — 7, собак — 2;
• На 2 этаже 12 собак и кошек. Кошек на 4 больше, чем собак. Ответ: кошек — 8, собак — 4;
• На 3 этаже 13 собак и кошек. Кошек на 5 больше, чем собак. Ответ: кошек — 9, собак — 4;
• На 4 этаже 15 собак и кошек. Кошек на 1 больше, чем собак. Ответ: кошек — 8, собак — 7;

Задача для 3 и 4 класса.

• На 1 этаже 13 собак и кошек. Кошек на 1 больше, чем собак. Ответ: кошек — 7, собак — 6;
• На 2 этаже 14 собак и кошек. Кошек на 4 больше, чем собак. Ответ: кошек — 9, собак — 5;
• На 3 этаже 170 собак и кошек. Кошек на 30 больше, чем собак. Ответ: кошек — 100, собак 70;
• На 4 этаже 140 собак и кошек. Кошек на 20 больше, чем собак. Ответ: кошек — 80, собак 60;

Набор варенья

Надо найти определённое количество способов, чтобы набрать заданный вес варенья. КГ — это килограммы; ШТ — это штуки.

Задача для 1 класса Найди ВСЕ способы набрать 6 кг варенья. Ответ: 1х6, 1х4+2х1, 1х2+2х2, 2х3, 1х1+2х1+3х1, 3х2, 3х1+1х3.

Задача для 2 класса Найди ВСЕ способы набрать 9 кг варенья. Ответ: 1х9, 1х6+1х3, 2х3+3х1, 3х3, 1х4+1х3+1х2, 1х4+1х5, 2х4+1х1.

Задача для 3 класса Найди ВСЕ способы набрать 10 кг варенья. Ответ: 1х10, 1х7+3х1, 1х4+3х2, 3х3+1х1, 1х5+5х1, 5х2, 1х2+3х1+5х1.

Задача для 4 класса Найди ВСЕ способы набрать 12 кг варенья. Ответ: 1х12, 1х8+4х1, 1х4+4х2, 4х3, 1х2+4х1+6х1, 1х6+6х1, 6х2.

Где клад?

Прочитай таблички и выбери сундук, в котором спрятан клад. Только на одной из табличек правда. Задача для 1 класса:

• 1 сундук — клад тут 2 сундук — тут клада нет 3 сундук — клад в первом сундуке. Так как таблички первого и второго сундука утверждают, что клад в 1 сундуке, а по условию только одна табличка правильная, то клада в 1 сундуке быть не может. Соответственно, если таблички с 1 и 3 сундука врут, значит на втором сундуке говорит правду, т.е. во 2 сундуке нет клада. А раз в 1 и 2 сундуке нет клада, то значит он в 3 сундуке!

• Прочитай таблички и выбери сундук, в котором спрятан клад. На одной из табличек неправда. Задача для 2 класса 1 сундук — клад тут 2 сундук — тут клада нет 3 сундук — клад не во втором сундуке В отличии от первого класса, тут одна табличка не верная, читаем вторую и третью таблички, которые утверждают, что во 2 сундуке нет клада, а раз они дублируют утверждение, значит они верны и именно там нет клада. Теперь первая табличка «клад тут», значит это неправда., поэтому в 1 сундуке нет клада. Верный ответ — 3 сундук.

• Прочитай таблички и выбери сундук, в котором спрятан клад. На одной табличке правда, на другой ложь, а ещё про одну мы не знаем. Задача для 3 класса 1 сундук — клад не во втором сундуке 2 сундук — тут клада нет 3 сундук — клад тут С этим заданием надо повозится, я бы советовал пойти от обратного, предполагать, что в сундуке клад и уже от этого сравнивать указания на табличках. 1 сундук — первая табличка правда, вторая правда, третья ложь. 2 сундук — первая ложь, вторая ложь, третья ложь. 3 сундук — первая правда, вторая правда, третья правда. Теперь понимаете, что делать надо? Два последних варианта никак не подходят, значит первый вариант верный.

• Прочитай таблички и выбери сундук, в котором спрятан клад. На каждом сундуке одна табличка с правдой и одна с ложью. Задача для 4 класса 1 сундук — клад не в третьем сундуке, тут клада нет 2 сундук — клад не в первом сундуке, клад тут 3 сундук — клад не во втором сундуке, тут клада нет Пойдём по пути предполагаемого нахождения клада в сундуке. Начну сразу с третьего сундука, 1 и 2 вы сможете сами проверить. Таблички первого сундука ложь+правда, второго — правда+ложь, третьего — правда+ложь. Это выполняет условиям задания.

Призовой фонд

За участие в олимпиаде каждый ученик получает сертификат, грамоту или диплом. Сертификаты получают все дети, решившие хотя бы одну задачу, но набравшие меньше баллов, чем 33% участников. Если результат лучше, чем у 33% всех участников, то ребенку отправляют похвальную грамоту. Если результат лучше, чем у 66% участников, то такой ученик считается победителем, и он награждается дипломом.

Просмотров:
1 346

образовательных олимпиад.

• Образовательные олимпиады
• Летние школы
• Подготовительное отделение
• Изучение английского языка
• Бакалавриат
• Магистратура
• Послевузовское образование
• ИТ-образование
• Медицинское образование
• Инженерное образование

© Депозитфото

Образовательная олимпиада — интеллектуальное соревнование среди абитуриентов, дающее реальный шанс поступить в вуз после вступительных экзаменов и получить либо государственную стипендию, либо значительную скидку на обучение. Участие для абитуриентов абсолютно бесплатное.

Некоторые олимпиады проводятся исключительно для иностранных абитуриентов. Их цель – привлечь в Россию самых талантливых студентов. Обычно эти соревнования проводятся вузами при поддержке государственных организаций, объединений организаций образования и крупных государственных корпораций.

В России тоже есть целая система олимпиад для старшеклассников. В некоторых из них могут принять участие абитуриенты из других стран. Олимпиады бывают I, II или III уровня в зависимости от масштаба и сложности задач. Призы также различаются. Это может быть поступление в вуз без вступительных экзаменов, максимальный балл ЕГЭ (единый государственный экзамен Российской Федерации) по предмету олимпиады или государственная стипендия (квота) на обучение. Обратите внимание, что участие в этих олимпиадах часто требует высокого уровня владения русским языком.

Как правило, все олимпиады проводятся в два основных этапа – отборочный и соревновательный. Каждый из них можно разделить на несколько внутренних шагов. Этап отбора начинается с подачи онлайн-портфолио, а затем участники проходят собеседование с комитетом. Конкурсный этап может включать в себя отдельные конкурсные треки и предметы. До 2020 года многие олимпиады проводились в основном в офлайне. Можно было подать заявку дистанционно, но само участие требовало личного присутствия. В связи с ограничениями в условиях пандемии правила изменились. Теперь вы можете пройти квалификацию, принять участие и выиграть онлайн, не покидая своей страны.

© Depositphoto

Олимпиады для иностранных абитуриентов

Open Doors: Russian Scholarship Project Международная олимпиада

Организатор: Ассоциация мировых университетов при поддержке Россотрудничества и Министерства науки и высшего образования Российской Федерации.

Уровень образования: степень магистра, докторантура.

Участники: гражданина любой страны и лица без гражданства, в том числе россияне, проживающие за рубежом, имеющие степень бакалавра или специалиста.

Направления
Магистерская программа: биология и биотехнология, информатика и наука о данных, математика и искусственный интеллект, бизнес и менеджмент, политология, нейробиология и психология, физические науки, лингвистика и современные языки, химия и материаловедение, экономика и эконометрика, техника и технологии, клиническая медицина и здравоохранение, науки о Земле, образование.
Кандидат наук: биология и биотехнология, клиническая медицина и здравоохранение, лингвистика и современные языки, математика и искусственный интеллект, физические науки, химия и материаловедение.

Формат: онлайн.

Этапы: 2 основных этапа – конкурс портфолио и решение задач по выбранной тематике. Для направления PhD предусмотрен 3-й этап – собеседование с потенциальным научным руководителем.

Победители получают возможность поступить в один из 500 вузов России без вступительных экзаменов и учиться бесплатно.

Глобальный стипендиальный конкурс НИУ ВШЭ

Органайзер: Национальный исследовательский университет «Высшая школа экономики» при поддержке Россотрудничества.

Уровень образования: степень бакалавра.

Участники: иностранных учащихся выпускных классов средних школ и колледжей, а также студенты и выпускники зарубежных вузов в возрасте до 30 лет.

Направления: Английский язык, востоковедение, дизайн, журналистика, история, культурология, математика, медиакоммуникации, международные отношения, право, психология, реклама и связи с общественностью, современная политика, социальные науки, физика, филология, философия.

Формат: онлайн и офлайн.

Этапы: один этап включает в себя решение задач по выбранному направлению. Вы можете участвовать в олимпиаде лично в своей стране или онлайн.

Победители и призеры получат полную или частичную стипендию Правительства Российской Федерации и скидки на обучение по программам бакалавриата НИУ ВШЭ.

© Depositphoto

Международные открытые олимпиады по математике и информатике для школьников и выпускников

Организатор: Университет ИТМО

Уровень образования: степень бакалавра или специальность.

Участники: иностранных граждан – аспирантов, а также выпускников школ.

Предметы: математика, информатика.

Формат: онлайн и офлайн.

Этапы: квалификации проходят онлайн, а финалы – очно или онлайн.

Победители получат возможность получить государственную стипендию (квоту) для поступления не только в Университет ИТМО, но и в любой вуз России на обучение по техническим программам бакалавриата или специалитета.

Физтех.Международный

Организатор: Московский физико-технический институт при поддержке Россотрудничества.

Уровень образования: степень бакалавра.

Участники: иностранных граждан выпускных классов.

Направления: физика, математика, биология – можно выбрать несколько направлений.

Формат: онлайн и офлайн.

Этапы: первый отборочный этап Олимпиады пройдет онлайн, второй – офлайн одновременно в нескольких странах.

Победители: выпускников школы получат дополнительные баллы за поступление в МФТИ и возможность участия в финале Физтех-олимпиады, а также рекомендацию на получение государственной стипендии (квоты) в МФТИ. Школьники автоматически проходят в финал Физтех.Международной или Физтех-олимпиад в следующем году.

Олимпиады для иностранных и российских абитуриентов

Российская олимпиада школьников высшей пробы

Организатор: Национальный исследовательский университет «Высшая школа экономики».

Уровень образования: степень бакалавра.

Участников: школьников вне зависимости от гражданства.

Направления: биология, востоковедение, восточные языки, география, дизайн, журналистика, международные языки, информатика, история, история мировых цивилизаций, культурология, математика, обществознание, основы бизнеса, политология, право, психология, русский язык , социология, физика, филология, философия, финансовая грамотность, химия, экономика, электроника и вычислительная техника.

Формат: онлайн, офлайн.

Этапов: отборочных онлайн, основной – оффлайн.

победителей и призеров получат льготы при поступлении в НИУ ВШЭ и другие вузы РФ.

Сибирская олимпиада школьников

Организатор: Новосибирский национальный исследовательский государственный университет.

Уровень образования: степень бакалавра.

Участники: школьников 7–11 классов вне зависимости от гражданства.

Направления: информатика, химия, физика, математика, биология, астрономия.

Формат: онлайн, офлайн.

Этапов: два отборочных (онлайн и офлайн) и финальный (оффлайн). Оффлайн-этапы проходят в России, Казахстане и Узбекистане.

победителей  могут получить льготы при поступлении в НГУ и другие вузы России.

© Depositphoto

Инженерная олимпиада школьников

Организатор: Национальный исследовательский ядерный университет «МИФИ», РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА, НГТУ им. Р.Е. Алексеева, Самарский университет, СПбГЭТУ ЛЭТИ, БГТУ им. В.Г.Шухова, ВлГУ в партнерстве с АО «Концерн Росэнергоатом».

Уровень образования: степень бакалавра.

Участники: учащихся 9–11 классов, в том числе граждане других государств.

Направления: задачи по физике с инженерным углом.

Формат: онлайн, офлайн.

Этапы: онлайн-отборочный этап и оффлайн-финальный этап.

победителей  могут получить льготы при поступлении в вузы-организаторы и другие вузы России.

КФУ Межрегиональные предметные олимпиады

Организатор: Казанский федеральный университет.

Уровень образования: степень бакалавра.

Участники: школьников выпускных классов, граждан Российской Федерации, Казахстана, Кыргызстана, Таджикистана, Белоруссии.

Направления: Программы бакалавриата КФУ по различным направлениям.

Формат: онлайн, офлайн.

Этапы: онлайн-отборочный этап, оффлайн-основной этап.

победителей получают льготы при поступлении на программу бакалавриата КФУ.

Я магистерская олимпиада КФУ

Организатор: Казанский федеральный университет.

Уровень образования: Степень магистра.

Участники: студентов или выпускников бакалавриата или специалитета последних курсов, граждан Российской Федерации, Казахстана, Кыргызстана, Таджикистана, Беларуси.

Направления: большинство магистерских программ КФУ по различным направлениям.

Формат: онлайн, офлайн.

Этапы: онлайн-отборочный этап, оффлайн-основной этап.

Победители получают льготы при поступлении в магистратуру КФУ.

Олимпиада «Технокубок» по программированию для школьников

Организатор: Московский физико-технический институт и МГТУ им. Баумана.

Уровень образования: степень бакалавра.

Участников:  школьники 8–11 классов, граждане Российской Федерации и других стран.

Направления:  : информатика.

Формат: онлайн, офлайн.

Этапы: онлайн-отборочный этап, оффлайн-основной этап.

победителей и призеров получают льготы при поступлении в большинство технических вузов России.

© Depositphoto

Олимпиада Высшей лиги для студентов и выпускников

Организатор: Национальный исследовательский университет «Высшая школа экономики»

Уровень образования:  Степень магистра.

Участников: студентов бакалавриата, выпускников бакалавриата или специалитета из любой страны.

Направления: 38 направлений обучения.

Формат: онлайн, офлайн.

Этапы: онлайн-отборочный этап и основной этап 2-х офлайн-конкурсов: по выбранному направлению и по выбранному треку.

победителей и призеров получают льготы при поступлении на ранее выбранную магистерскую программу НИУ ВШЭ.

Олимпиада Физтех

Организатор: Московский физико-технический институт.

Уровень образования: степень бакалавра.

Участники: старшеклассника из России, Армении, Белоруссии, Казахстана, Киргизии, Молдовы, Таджикистана, Туркменистана, Узбекистана, Украины, а также победители Международной олимпиады Физтех.

Предметы: физика, математика, биология.

Формат: онлайн и офлайн.

Этапы: онлайн-отборочный этап, офлайн-основной этап по выбранной тематике.

Победители International могут получить квоту на бесплатное обучение в МФТИ.

Росатом Физико-математическая олимпиада школьников

Организатор: Национальный исследовательский ядерный университет «МИФИ» совместно с Госкорпорацией «Росатом», ВГУ, КАИ, НГТУ им. Р.Э. Алексеева, УрФУ.

Уровень образования: степень бакалавра.

Участники: школьников 7–11 классов, в том числе граждане других стран.

Направления: математика, физика.

Формат: онлайн, офлайн.

Этапы: онлайн отборочный этап, оффлайн финальный этап.

победителей  могут получить льготы при поступлении в вузы-организаторы и другие вузы России.

Перед тем, как зарегистрироваться на сайте этих олимпиад, не забудьте внимательно ознакомиться с правилами и при необходимости уточнить детали у организаторов.

При поступлении в российский вуз учитываются не только победы на олимпиадах, но и участие в личных и командных соревнованиях международных или национальных соревнований. Этим успехам приемная комиссия вуза уделит особое внимание.

Выиграть Олимпиаду вполне возможно! Во-первых, внимательно подойдите к процессу подготовки и подачи портфолио. Российские вузы ищут талантливых студентов со всего мира. Приз в олимпиаде позволяет получить высшее образование, полностью или частично оплачиваемое Российской Федерацией. Следите за новостями об открытии регистрации на различные олимпиады, подавайте заявки сразу на несколько конкурсов и треков, тренируйтесь в выполнении тестовых заданий, предоставленных организаторами, и никогда не сомневайтесь в своих силах!

Математический блог Тани Ховановой » Архив блога » Зачем американцам учиться на Московских математических олимпиадах

16 февраля 2012, 10:49

Я уже писала о том, что американские математические соревнования нелогично устроены, к первым турам не готовятся студентов для более поздних туров. Впервые математики сталкиваются с пруфами на третьем уровне USAMO. Как они могут подготовиться к задачам с доказательствами? Я предлагаю смотреть на восток. Все туры всероссийских математических олимпиад — от местных до региональных и всероссийских — устроены одинаково: в них есть несколько задач, требующих доказательств. Это похоже на USAMO. На национальной Всероссийской олимпиаде уровень сложности такой же, как USAMO, а на региональных проще. Это делает задачи от регионалов отличным способом тренировки для USAMO. Лучшая региональная олимпиада в России – Московская олимпиада. Вот проблема от 1995 Московская олимпиада:

Начнем с четырех одинаковых прямоугольных треугольников. За один ход мы можем разрезать один из треугольников по высоте, перпендикулярной гипотенузе, на два треугольника. Докажите, что после любого количества ходов среди всего множества найдутся два одинаковых треугольника.

Этот тип задач очень отличается от тех, которые вы найдете в AMC и AIME. Ответ не число; скорее, проблема требует доказательств и изобретательности, и догадки не могут помочь.

Еще одна задача с олимпиады 2002 года. В данном конкретном случае задачу нельзя адаптировать к множественному выбору:

Тангенсы углов треугольника — целые положительные числа. Каковы возможные значения этих касательных?

Задачи взяты из двух книг: Московские математические олимпиады 1993-1999 гг. и Московские математические олимпиады 2000-2005 гг. Я люблю эти книги и задачи, которые в них представлены с прошлых московских олимпиад. Решения красиво написаны, и книги часто содержат альтернативные решения, расширенное обсуждение и интересные замечания. Кроме того, некоторые задачи проиндексированы по темам, что очень удобно для таких учителей, как я. Но самое лучшее в этих книгах — это сами проблемы. Посмотрите на следующую жемчужину 2004 года, которую можно использовать как фокус или идею для исследовательской работы:

Колода из 36 игральных карт (четыре масти по девять карт в каждой) лежит перед экстрасенсом лицевой стороной вниз.