Магнитный конструктор схемы: Поделки из магнитного конструктора

Содержание

Поделки из магнитного конструктора — фото и картинки: 76 штук

Магнитный конструктор схемы сборки

Магнитный конструктор схемы сборки краб

Магнитный конструктор схемы

Магнитный конструктор схемы сборки

Магнитный конструктор Магникон схемы

Схемы по сборке магнитного конструктора

Магнитный конструктор 3д Магнетик объемный видеообзор

Bornimago магнитный конструктор схемы

Магнитный конструктор инструкция по сборке схемы

Постройки из магнитного конструктора

Магнитный конструктор 102 детали

Магникон конструктор схемы сборки

Магнитный конструктор Chao le XING mag-Cube mag014

Магнитный конструктор Magformers Standart 63070-62

Магнитный конструктор схемы сборки краб

Magnetic Blocks Intelligence 62 PCS

Магнитный конструктор ГЕОМАКС

Magic Magnetic Blocks конструктор

Магформерс инструкция по сборке схемы

Магнитный конструктор Power Clix

Магнитный конструктор Magformers схемы сборки

Магнитный конструктор Магформерс схемы сборки

Магнитный конструктор для детей на прозрачном фоне

Магникон схемы сборки

Магформерс конструктор 115

Магнитный конструктор Xinbida Magnetic Buildung Blocks 8221

Геометрические фигуры из магнитного конструктора

Магформерс динозавры

Магформерс шар схема

Manyetik LEGO

Neoformers магнитный конструктор

Магнитный конструктор из шариков и палочек схемы

Магформерс динозавр игрушки

Magnetic Sticks for Flashcards

Магнитный конструктор Magformers динозавры

Магформерс «Smart Set»

Магнитный конструктор Магформерс «Neon Color Set», 60 деталей 63110

Конструктор магнитный робот Магнетик

Конструктор магнитный i169-h36004

Магнитный конструктор Магникон схемы

Магнитный конструктор Geomag Color — 60

Головоломка конструктор магнитные фигуры

Схемы для магнитного конструктора Magnetic Blocks

Конструктор магнитный «Geomag glitter», 68 деталей

Магнитный конструктор Magformers Deluxe 710009 супер

Магнитный конструктор Magformers 63077 Challenger Set

Магнитный конструктор Geomag Kids Color 216

Magformers 710012

Magformers Creative 90

Магнитный конструктор Magformers Standart 60008 прямоугольники

Магнитный конструктор Магформерс динозавр

Магнитный конструктор Mini Magical Magnet 58

Магнетик Блокс конструктор

Магформерс Expert Set

Магнитный конструктор Игруша

Магнитный конструктор схемы

Магнитный конструктор Magnetix

Конструктор Magnetic Blocks 56 деталей

Mag-building 96 деталей

Магнитный конструктор mag building, 58 деталей

Magnetic Blocks конструктор

Магнитный конструктор Magnetic Blocks

Магнитный конструктор Полидрон схемы

Магнитный конструктор mag-building GB-w200 Smart Set

Конструктор магнитный (44 дет) в коробке

Фигурки для магнитного конструктора

Конструктор Магникон МК-200

Магнитный конструктор Магникон динозавры

Магнитный конструктор Magformers creator 62

Магникон Луноход MK-40

Поделки из магнитного конструктора

что сделать из треугольников и квадратов, картинки, схемы фигурок и поделок, которые можно построить, цена,

Приветствую всех читателей ресурса, сегодня я хотел бы представить вашему вниманию довольно качественный и очень увлекательный магнитный конструктор. Если кратко- очень рекомендую, а за подробностями прошу под кат.

Некоторое время назад, да и сейчас пожалуй, среди всевозможных конструкторов были замечены необычные и интересные наборы пластиковых форм со встроенными магнитами, в народе они называются магформерсами (Magformers). Подробную информацию о конструкторах можно найти на сайте производителя.

Наборы таких конструкторов состоят преимущественно, из различных геометрических фигур (треугольники, квадраты, трапеции, тетраэдры, и вовсе уж замысловатые фигуры), в которые встроены маленькие, но крайне эффективные неодимовые магниты. Также обычно вкладываются различные вспомогательные элементы- платформы, колеса, стойки и прочее.

На сайте производителя имеется информация, что все элементы изготовлены из HQABS пластика (высококачественный ABS пластик), и не содержат каких-либо опасных веществ. А благодаря ультразвуковой сварке, неодимовые магниты абсолютно безопасны для детей.

Все бы хорошо, но вот цены… с ними можно ознакомится на сайте официальных представителей в России.

К счастью, братья- китайцы очень быстро сориентировались и выпустили в продажу свои конструкторы, внешне и функционально ничем не отличающиеся от пресловутых магформерсов. Вот один из таких наборов- Magnetic Toy 138 Pieces Plastic Building Blocks мне и выпала удача оценить.

Доставили конструктор быстро, но не очень аккуратно- коробка была изрядно помята (Пони экспресс отличились).

Коробка очень приличная- красочная полиграфия и тематические слоганы на ней создают впечатление качественного и продуманного товара. Неповрежденной она смотрелась бы еще лучше, жаль, что она всего лишь картонная, а не титановая антивандальная.

На одной из боковых сторон находится картинка со всеми видами фигур, которые можно найти в конструкторе. Далее располагается стилизованная голова с лампочкой «озарения», а под ней пояснительная надпись — «Воображение». Ну, а ниже можно прочесть надписи «Счастливое время» и призыв к улучшению интеллектуальной и созидательной деятельности с помощью данного конструктора.

На лицевой же стороне находятся несколько примеров того, что можно собрать из конструктора, три пиктограммки, каждая имеет сопроводительную надпись- «Воображение», «Созидание» и «Координация рук», а также название конструктора и слоган- «Магнитные блоки, разрушь обыденность!». Причем глагол Break (разрушать) начитается на букву, очень похожую на E — думаю, это такая задумка дизайнеров, а не банальная безграмотность, так как весь остальной текст без ошибок.

Задняя сторона не изобилует элементами дизайна- только значки типа ресайклинг и все такое, опять таки слоган с неправильной би, ну и надпись «сделано в Китае»

На двух последних сторонах коробки изображены летательный аппарат и паровозик ( конечно же, построенные из деталей набора) и серия октаэдров, в которые вписано следующее:

● логическое мышление

● координация связки глаза- руки

● восприятие

● воображение

● созидание

● концентрация

Все эти качества ребенка и призван развить конструктор.

Комплектность:

А внутри изрядно покалеченной коробки обнаружилось вот что:

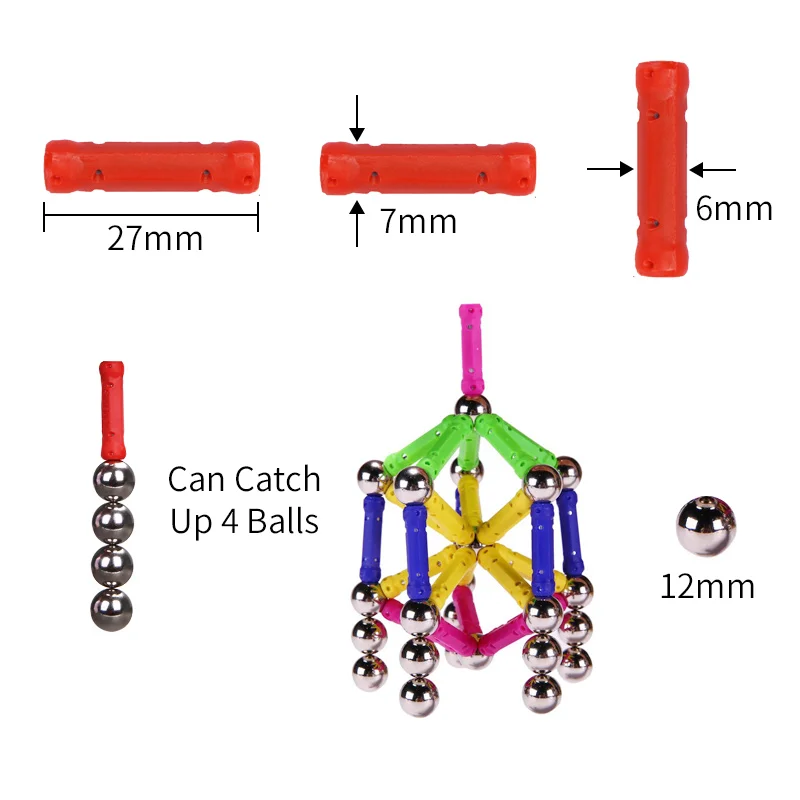
▪ сто тридцать восемь конструктивных элементов, бережно обмотанных пупыркой

▪ инструкция с примерами сборки некоторых интересных конструкций

В продаже имеется несколько комплектаций конструктора, вот сводная таблица деталей и их размеры, колонка нашего набора из 138 деталей подсвечена красным:

Больше всего оказалось треугольных элементов, что не удивительно, ведь это одна из наиболее универсальных геометрических форм, и из них можно в свою очередь, создать большое количество всевозможных конструкций.

Лидерами же по численности идут квадраты с цифрами, с их помощью можно создавать простые примеры и даже уравнения.

Кроме цифр и знаков арифметических действий в наборе оказались квадратики с фруктами, вопросительным знаком и буквой Кью (или крайне похожим на нее символом).

Также были в наличии и все вышеупомянутые элементы для создания ветряной мельницы и колеса обозрения, а также три транспортные платформы с колесами (шесть штук).

Количество предметов довольно внушительное, поэтому для их хранения пришлось выделить пластиковую коробку.

Первым делом просмотрел детали с магнитами — качество пластика на очень высоком уровне, облоев, шероховатостей нет, стыки практически незаметны, на вид части детали скорее склеены чем то типа дихлорэтана, а не сварены ультразвуком как их американские прототипы, хотя я не видел ранее качества ультразвуковой сварки и судить об этом не берусь. Разъединить их у меня не получилось, деталь начинала ломаться, а клей не поддавался.

Фото детали

Инструкция:

Инструкция оказалась на диво информативной и подробной, жаль, что только на английском. Но и по картинкам все интуитивно понятно и наглядно.

Вся подаваемая информация разделена на пять секций:

● аксессуары (тут описаны и наглядно представлены все имеющиеся в наборе детали конструктора)

● математические действия (приведены примеры использования конструктора в составлении простых примеров, уравнений и даже логических рядов, где необходимо найти закономерность и закончить ряд)

● двухмерное (плоскостное) конструирование, в этом разделе показано, как можно составлять различные фигурки на плоскости

● основное моделирование, тут уже мы имеем дело с пространственным, 3D конструированием

● и наконец, самый большой раздел отведен под примеры, в нем поэтапно расписано создание тех или иных конструкций, начиная от простейших кубиков и заканчивая колесом обозрения или впечатляющим роботом)

Ниже увеличенный и слегка переведенный фрагмент задач на математическую логику:

А вот так делается колесо обозрения:

Примеров масса, все их мы пока не собрали, а вот кое-что из уже собранного:

2D велосипед:

Фигвам с принцессами:

Два многогранника:

Транспортное средство:

Пример примера 🙂 (тавтология)

И наконец- колесо обозрения:

Видео сборки разных конструкций:

Подводя итоги:

Конструктор очень интересный, сделан качественно — играть с ним одно удовольствие. Рекомендуемый возраст ребенка- от 3 лет, самый же подходящий возраст по моему мнению- 4-5 лет, хотя мелкую моторику можно тренировать с его помощью гораздо раньше.

А вот математические и пространственные упражнения будет интересно выполнять ребенку постарше.

В настоящее время на данный набор установлена акционная цена, есть возможность купить его немного дешевле, чем обычно.

Всем спасибо за прочтение, всего наилучшего!

Товар для написания обзора предоставлен магазином. Обзор опубликован в соответствии с п.18 Правил сайта.

Руководство по проектированию магнитных цепей

| Технические примечания | Магниты

1. Основные расчетные формулы

1-1.

Полный магнитный поток Φ и электрическая проводимость P

Основная формула расчета для магнитных цепей аналогична закону Ома; а именно, когда полный магнитный поток обозначается через Φ,
магнитодвижущая сила через F, а магнитное сопротивление через R, соотношение между этими тремя элементами выражается следующей формулой: используется вместо магнитного сопротивления R.
Следовательно, приведенную выше формулу можно заменить следующей формулой:

Когда длина магнитного пути обозначается L, площадь поперечного сечения магнитного пути — A, а проницаемость магнитного пути — µ, магнитная проницаемость P выражается следующей формулой:

Эта формула показывает, что чем короче длина магнитного пути L и чем больше площадь поперечного сечения А и проницаемость μ, тем больше проницаемость Р (т.е. меньше магнитное сопротивление).

Кроме того, проницаемость Pt для всей магнитной цепи выражается суммой проницаемости зазора Pg, которая определяется как величина, обратная магнитному сопротивлению в зазоре, и проницаемость рассеяния Pf определяется как величина, обратная магнитному сопротивлению, вызванному магнитным потоком рассеяния ( Pt = Pg + Pf ).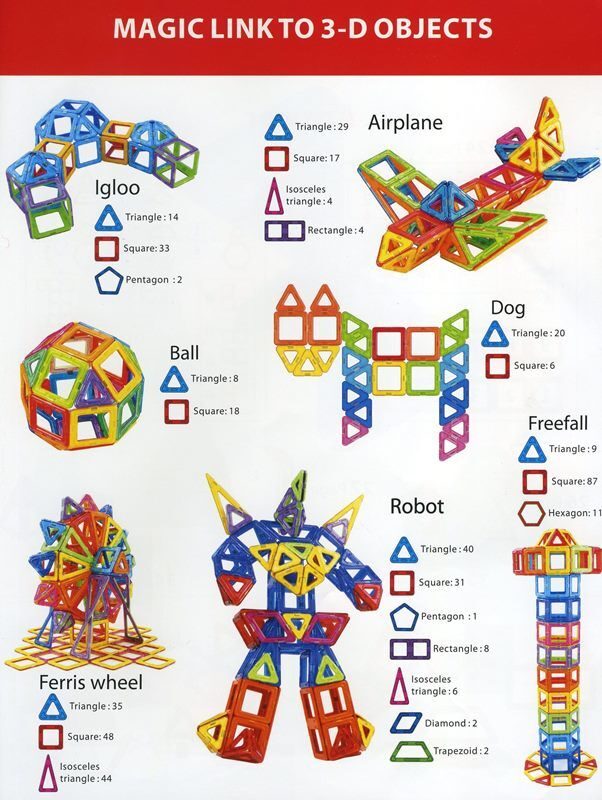

Чтобы понять поток рассеяния для каждого пространства магнитного пути, общая магнитная проницаемость Pt выражается как сумма проницаемости зазора Pg и магнитной проницаемости каждого пространства магнитного пути (Pf ₁ + Pf ₂ + Pf ₃ + ……. Pf _n ).

1-2. Коэффициент потерь магнитодвижущей силы f

Коэффициент потерь магнитодвижущей силы f определяется как отношение полной магнитодвижущей силы F
магнитопровод к зазору магнитодвижущая сила Fg.

Общая магнитодвижущая сила F магнитной цепи определяется используемым магнитом, а ее значение является произведением напряженности магнитного поля в точке
рабочая точка магнита Hd и длина магнита Lm.
Кроме того, магнитодвижущая сила зазора Fg является произведением плотности магнитного потока зазора Bg и длины зазора Lg; следовательно, формулу (5) можно расширить до следующей формулы:

1-3. Коэффициент рассеяния σ

Коэффициент рассеяния выражается отношением полного магнитного потока Φt, создаваемого магнитом в магнитопроводе, к сходящемуся в зазоре магнитному потоку Φg.

Полный магнитный поток Φt, создаваемый магнитом, определяется как произведение плотности магнитного потока в рабочей точке Bd и поперечного сечения магнита
площадь сечения Am, а магнитный поток, сходящийся в зазоре Φg, определяется как произведение плотности магнитного потока Bg зазора на площадь поперечного сечения зазора
Аг; поэтому формулу (7) можно расширить до следующей формулы:

Кроме того, из формулы (2) :Φ = FP формула (7) также может быть выражена следующей формулой:

Поскольку коэффициент потерь магнитодвижущей силы f обычно становится значением, близким к 1, Формула (9) станет следующей формулой путем замены формулы (5) и формулы (4):

Эту формулу также можно выразить в следующей форме, разделив Pf на каждое пространство магнитного пути рассеяния:

1-4. Коэффициент проницаемости Pc

Коэффициент проницаемости Pc используется для выражения рабочей точки магнита на кривой B-H. Эта величина определяется как отношение плотности магнитного потока Bd к напряженности магнитного поля Hd в
рабочей точки и выражается следующей формулой (см. рисунок выше):

1-4-а. Коэффициент магнитной проводимости магнита, включенного в магнитную цепь

Коэффициент магнитной проводимости магнита, включенного в магнитную цепь, можно определить, получив Hd и Bd из формул (6) и формул (8) и подставив их в формулу (11).

И заменив это на　

, можно получить следующую формулу:

1-4-б. Коэффициент магнитной проводимости цельного магнита

На коэффициент магнитной проводимости одиночного магнита в значительной степени влияет форма магнита, поэтому очень сложно получить точное значение расчетным путем.
Таким образом, из приведенного ниже рисунка с использованием столбчатого магнита в качестве образца (график, показывающий взаимосвязь между отношением размеров и коэффициентом магнитной проводимости) получена грубая оценка.

Формула приближения будет следующей:

1-5. Методы расчета длины Lm, площади поперечного сечения Am и объема Vm

Длина Lm и площадь поперечного сечения Am, необходимые для магнита, составляют

. необходимые Lm и Am могут быть получены.
И необходимый Vm равен

, что указывает на то, что необходимый объем магнита обратно пропорционален произведению энергии в рабочей точке.

1-6. Метод определения коэффициента утечки σ и коэффициента потерь магнитодвижущей силы f

1-6-a. Процедуры экспериментального получения σ и f

■ Метод с использованием поисковой катушки

1. Намотайте поисковую катушку на магнит и измерьте магнитный поток в зазоре.
2. Рассчитайте Bd из полного потока Φg/площади поперечного сечения магнита Am.
3. Получите Hd из кривой B-H (кривая размагничивания).
4. Измерьте Bg, Ag, Lg, Am и Lm.
5. Рассчитайте f и σ по формуле (6) и формуле (8).

■ Метод без использования поисковой катушки

1. Предположим, что значение f (обычно между 1,0 и 1,2).
2. Измерьте Lm, Bg и Lg.
3. Рассчитайте Hd по формуле (12) на предыдущей странице.
4. Получите Bd из кривой B-H (кривая размагничивания).
5. Измерьте Am и Ag и рассчитайте σ по формуле (8).

1-6-б. Метод получения σ расчетным путем

Получите Pg и Pf ₁ через Pf _n по формуле (10),

и вычислите σ.

Справочный пример

Пример расчета магнитной проницаемости основных компонентов (Pg, P ₁ , P ₂ P ₃ и P ₄ ) пространства пути магнитного рассеяния показан ниже.

1) Проницаемость площади зазора на рисунке

2) Проницаемость полуцилиндрического магнитного пути рассеяния

3) Проницаемость полуцилиндрического (полого) магнитного пути рассеяния

4) Проницаемость четвертьсферического магнитного пути рассеяния

5) Проницаемость Полая четверть сферического магнитного пути рассеяния

Объединяя проницаемость вышеперечисленных пунктов с 1) по 5), можно получить грубую оценку σ в пространстве магнитного пути рассеяния ( μ ₀ : проницаемость вакуума).

2. Формула расчета плотности магнитного потока B(X) на центральной линии магнита

Когда кривая B-H прямая или рабочая точка Bd расположена выше точки перегиба, распределение магнитного поля вне магнита может рассматривать так же, как магнитное поле, создаваемое замкнутым током на внешней периферийной поверхности пространства длиной X, имеющего такую же магнитную проницаемость и форму поперечного сечения, что и магнит.
Формулы расчета для получения этого B(X) для трех типичных форм будут показаны ниже. Эти формулы эффективны в качестве аппроксимационных формул для ферритовых магнитов или неодимовых магнитов.

2-1. Магнит цилиндрической формы

2-2. Магнит в виде квадратной стойки

2-3. Трубчатый магнит

2-4. Когда магнитное тело находится за магнитным полюсом

Подставьте 2L в член L формул 2-1, 2-2 и 2-3.

2-5. Когда магниты одинаковой формы расположены напротив друг друга на расстоянии 2X

, B(X) в центре зазора станет в два раза больше, чем B(X), полученное с использованием формул 2-1, 2-2 и 2-3.
B(X) в точке P внутри промежутка будет суммой B(X-P), в которой X-P подставлен в член X предыдущей формулы, и B(X+P), в котором X+P вставлен в член X предыдущей формулы.

2-6. Когда магнитное тело расположено за магнитным полюсом в той же конфигурации, что и в предыдущем разделе

Подставьте 2L в член L формул 2-1, 2-2 и 2-3. B(X) в центре зазора и точка P внутри зазора могут быть получены с помощью тех же процедур, что и 2-5.

3. Расчет эффективного магнитного потока магнитных цепей для двигателей

В магнитных цепях для двигателей состояние магнитной цепи широко варьируется в зависимости от элементов, включая количество пазов ротора, форму пазов,
и толщина стенки корпуса. Поэтому в этом разделе будут показаны только формулы, которые показывают основные понятия.

1) Площадь поперечного сечения магнита Am

2) Отношение эквивалентных размеров магнита л/д

3) Коэффициент магнитной проводимости одиночного магнита Pi

4) Коэффициент магнитной проводимости одиночного магнита, включая ярмо PL

5) Коэффициент Кертера К _с

6) Эффективный коэффициент магнитной проводимости P _u

7) Магнитный поток рассеяния σ

8) Магнитный поток насыщения полюсов (или Эффективный магнитный поток) 00 90 07 О 90 07 магнитная цепь
Приведенный выше метод расчета Φg не принимает
с учетом насыщения магнитопровода. Однако в реальных магнитных цепях насыщение может происходить в области корпуса или ротора.
Другими словами, когда Φg, полученное вышеуказанным методом расчета, и Φg в реальном двигателе сравниваются, а g в реальном двигателе меньше расчетного значения, возможно, что магнитная цепь насыщается.

Таблица преобразования единиц СИ/СГС

Путем умножения характеристического значения в единицах СИ на коэффициент преобразования, указанный слева от ▶, можно получить значение в единицах СГС.
Аналогично, путем умножения характеристического значения в единицах СГС на коэффициент пересчета справа от ◀ можно получить значение в единицах СИ.

руб.

Единица СИ▶					◀Установка CGS
Магнитный терм	Символ изделия	Название устройства	Символ блока	Коэффициент преобразования▶	◀Коэффициент преобразования	Символ блока	Название устройства
Магнитный поток	Ф	Вебер	Вб	10 ⁸ ▶	◀10 ^-8	Мх	Максвелл
Плотность магнитного потока	Б	Тесла	Т	10 ⁴ ▶	◀10 ^-4	Г	Гаусс
Магнитное поле	Х	Ампер/м	А/м	4π×10 ^-3 ▶	◀10 ³ /4π	ОЕ	Эрстед
Намагничивание	М	Ампер/м	А/м	10 ^-3 ▶	◀10 ³	Г	Гаусс
Магнитная поляризация	Дж	Тесла	Т	10 ⁴ /4π▶	◀4π×10 ^-4	Г	Гаусс
Магнитодвижущая сила	FM	Ампер	А	4π×10 ^-1 ▶	◀10/4π	Ги	Гилберт
Сила магнитного притяжения	Ф	Ньютон	Н	10 ⁵ ▶	◀10 ^-5	дин	Дайн
Проницаемость	мк	Генри/м	Н/м	10 ⁷ /4π▶	◀4π×10 ^-7	Безразмерный
Проницаемость вакуума	мк ₀	4π×10 ^-7 Генри/м	Н/м			Безразмерный	1
Магнитное сопротивление		1/Генри	Н ^-1	4π×10 ^-9 ▶	◀10 ⁹ /4π	Ги/Мкс	Гилберт/Максвелл
Проницаемость	Р	Генри	Х	10 ⁹ /4π▶	◀4π×10 ^-9	Мкс/Ги	Максвелл/Гилберт
Продукт магнитной энергии	БХ	Дж/м ³	Дж/м ³	4π×10▶	◀10 ^-1 /4π	Г · ОЕ	Гаусс · Эрстед
Продукт магнитной энергии	БХ	Дж/м ³	Дж/м ³	10▶	10 ^-1	эрг/см ³	Эрг/см ³

Проектирование магнитных цепей

Опыты с магнитами
и наше окружение

Проектирование магнитных схем

Проектирование цепей с магнитными полями очень похоже на
проектирование электрических цепей.

В простых электрических цепях мы используем ЭДС (напряжение
источник) и резисторы, и может определить, какой ток будет течь.
Точно так же для магнитных цепей мы используем МДС и сопротивление материалов, и
можно определить, сколько потока будет течь.
См. Магнитные основы.

Вот ссылки, которые помогут вам узнать о конструкциях магнитных цепей,
и может предоставить вам детали и примеры.

http://www.magnetsales.com/
http://www.magnetsales.com/Magnet_Design.htm
http://www.magnetsales.com/Design/DesignG.htm
http://www.magnetsales.com/Design/Glossary.htm

http://www.dextermag.com/
http://www.dextermag.com/resource-center/document-library

http://www.usneodymiummagnets.com/
http://www.usneodymiummagnets.com/calculator.html

Ознакомьтесь со всеми разделами, посвященными рекомендациям по проектированию.

Это отличный учебник, как и все вышеперечисленные сайты.
Поваренная книга Raggio по дизайну электромагнита

Магнитные удостоверения

Ниже приведены различные тождества для этих магнитных терминов, и
их единицы.
Используйте тот, у которого есть информация, которую вы знаете.

Типичная проблема

Часто вам нужно создать схему, которая будет производить
определенное количество потока в воздушном зазоре.
Эта задача ниже может быть использована в качестве первого прохода.

Пример решения:

Пусть
A = 1 см x 3 см = 3*10 ^-4 м ²
lc = 60 см = 0,6 м

lg = 1 мм = 1*10 ^-3 м

N = 500 витков

B = 1,1 T

Мы будем использовать листовую сталь в качестве основного материала, поэтому нам понадобится B-H
Кривая для этого материала.

Из таблицы видно, что для данного типа стали:

Hc = 600 ат/м при B = 1,1 Тл

Hg = B/ ₀ = 0,9 / 4*pi*10 ^-7
= 716,2*10 ³ Ат/м

MMFc = Hc*lc = 600 * 0,6 = 360 при

MMFg = Hg*lg = 716,2*10 ³ * 1*10 ^-3
= 716,2 В

ММФт = 1076,2 В

i = MMFt / N = 1076,2 / 500 = 2,15 А

Итак, при токе 2,15А на 500 витков обмотки, при
этого конкретного типа стали, вы увидите что-то близкое к 1,1 Тл в пределах
воздушный зазор.

Если в схеме действительно было два воздушных зазора, просто добавьте два
вместе и смоделируйте его с одним большим воздушным зазором. Одна вещь, которая делает также
случается, что в воздушном зазоре поток имеет тенденцию немного распространяться в
воздуха, занимая немного большую площадь. Таким образом, решение не является точным, но
близко, так как мы не учли эту окантовку.

Увеличенный воздушный зазор

Что произойдет, если воздушный зазор сделать в два раза больше, но
мы все еще хотели 1,1 Тл в воздушном зазоре?
lg = 2 мм = 2*10 ^-3 м

Hc то же

Hg это то же самое

MMFc это тот же

MMFg будет в два раза больше = 1432,4. При

ММФт = 1792,4 В

i = 1792,4 / 500 = 3,58 А

Ток должен быть на 167% больше, чтобы создать
та же плотность потока 1,1 Тл в большем воздушном зазоре!

Воздушный зазор меньшего размера

Что произойдет, если воздушный зазор сделать вдвое меньше, но
мы все еще хотели 1,1 Тл в воздушном зазоре?
lg = 0,5 мм = 5*10 ^-4 м